Respuesta del maíz a la fertilización nitrogenada por zonas de manejo
Publicado: 19 de agosto de 2015
Fuente: Susana Albarenque, Ricardo Melchiori (INTA EEA Paraná), Bruno Basso (Michigan State University), Octavio Pedro Caviglia (INTA - CONICET - FCA-UNER) Argentina
INTRODUCCIÓN
La agricultura de precisión enfrenta el desafío de cuantificar la variabilidad de los procesos y las propiedades del suelo, determinando donde y cuando estas son responsables de las variaciones en el rendimiento de los cultivos (Mulla y Schepers, 1997) para poder aplicar tecnologías y principios que permitan manejar la variabilidad espacio-temporal de los cultivos (Pierce y Nowak, 1999).
Los suelos de la provincia de Entre Ríos presentan un ambiente de variabilidad potencialmente alta por sus características reflejándose tanto en la heterogeneidad de los tipos de suelo a diversas escalas, así como en los efectos de interacción entre las características intrínsecas de los suelos, la topografía y la dinámica del agua en los ambientes ondulados. Existen antecedentes que han permitido identificar al grado de erosión y la baja fertilidad físico-química como las características que más claramente permiten diferenciar zonas por su productividad potencial (Melchiori, 2007).
Las zonas de diferente productividad o de manejo, representan subregiones dentro de los lotes que expresan una combinación relativamente homogénea de factores determinantes del rendimiento para los que resulta apropiada una proporción única de insumos (Doerge, 1999). Cada zona debe mostrar diferente respuesta del cultivo a los fertilizantes y a otros insumos, y estas respuestas necesitan ser confiablemente estimadas antes de tomar decisiones de manejo (Miao et al., 2006).
La evaluación de las posibles interacciones entre suelo, clima, y manejo del N implican la realización de numerosos experimentos de campo repetidos en el tiempo. Los modelos de simulación pueden ayudar a tomar decisiones sobre estrategias de aplicación de N teniendo en cuenta este tipo de interacciones (Rinaldi, 2004), acelerando el desarrollo de recomendaciones según zonas de manejo.
La evaluación de las posibles interacciones entre suelo, clima, y manejo del N implican la realización de numerosos experimentos de campo repetidos en el tiempo. Los modelos de simulación pueden ayudar a tomar decisiones sobre estrategias de aplicación de N teniendo en cuenta este tipo de interacciones (Rinaldi, 2004), acelerando el desarrollo de recomendaciones según zonas de manejo.
Existen diversos modelos de simulación que han sido evaluados y utilizados satisfactoriamente en diferentes lugares del mundo, entre ellos los más difundidos han sido los que integran el entorno DSSAT (Decision Support System for Agrotechnology Transfer) (e.g. CERES, Ritchie and Otter, 1985; Jones and Kiniry, 1986) y fueron creados para simular el crecimiento, desarrollo y rendimiento de distintos cultivos, incluyendo rutinas para estimar la dinámica del agua y del nitrógeno (Jones et al., 2003). El modelo SALUS (System Aproach to Land Use Sustainability) fue desarrollado a partir de CERES e incluye nuevos enfoques y algoritmos (Basso et al., 2012).
SALUS-Terrae es un modelo de simulación que ha sido diseñado para predecir la variabilidad espacial y temporal del balance hídrico, permitiendo el manejo apropiado el agua y al mismo tiempo identificar áreas susceptibles a la erosión hídrica (Basso, 2005). Contar con el modelo SALUS calibrado y validado localmente sería de suma utilidad al momento de emplear SALUS-Terrae para aplicaciones en agricultura de precisión y conservación de suelos.
Los objetivos del presente trabajo fueron: i) calibrar y validar el modelo de simulación de cultivos SALUS, y ii) simular la respuesta a largo plazo a la fertilización nitrogenada del cultivo de maíz por zonas de manejo
MATERIALES Y MÉTODOS
La calibración del modelo SALUS se llevó a cabo utilizando datos de un ensayo realizado en el campo experimental del INTA Parana (31° 50’ S; 60° 31’ W, 110 m.s.n.m) durante la campaña 2011. En el mismo, se delimitaron zonas de manejo utilizando el software MZA (Management Zone Analyst) en base a mapas de conductividad eléctrica, elevación y materia orgánica. Como resultado del análisis se obtuvieron 4 zonas de manejo (Figura 1). Se evaluaron tratamientos de disponibilidad de N (Nd, i.e. N disponible), dentro de cada una de las ZM, que incluyeron 4 niveles de Nd: 70 kg N ha-1 (Ni(0-60cm)+Nf), 140 kg N ha-1 (Ni(0-60cm)+Nf), 210 kg N ha-1 (Ni(0-60cm)+Nf) y un testigo (T) al que no se le aplicó N (Nd=Ni).
Donde Ni(0-60cm) es el contenido de N en el suelo (0-60cm), en forma de nitrato previo a la siembra y Nf el N agregado con el fertilizante. La validación se realizó con datos de rendimiento de 4 años de ensayos de fertilización nitrogenada conducidos en la EEA Paraná del INTA, tres de ellos (2009, 2011 y 2012) con tres niveles de N (0, 69, 138, y 138 +138 kg N ha-1 en V6); el otro ensayo (2006) incluyó cuatro niveles de N a la siembra (0, 50, 150 y 200 kg N ha-1).
La simulación de la respuesta del cultivo de maíz a la fertilización nitrogenada por zonas de manejo a largo plazo se realizó con un esquema experimental similar al utilizado en la calibración, con cuatro niveles de Nd a la siembra: 0, 70, 140 y 210 kg ha-1.
Se utilizaron datos diarios de temperatura (máxima y mínima), precipitación, y radiación global para un período de 41 años (1971-2012), empleando datos meteorológicos de la Estación Experimental del INTA Paraná. Los datos de suelo para caracterizar cada zona de manejo fueron obtenidos de la carta de suelos de la Experimental Paraná (Van Barneveld, 1972), las principales diferencias entre zonas de manejo en los archivos de suelo del modelo se debieron al grado de erosión,
susceptibilidad a la erosión y a la capacidad de almacenar agua en el perfil.
susceptibilidad a la erosión y a la capacidad de almacenar agua en el perfil.
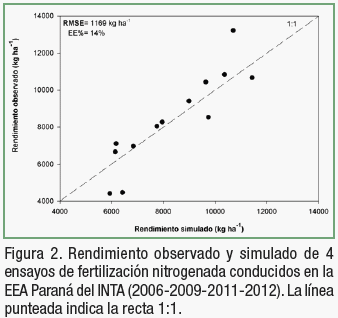
Se evaluaron las estimaciones del modelo mediante una regresión lineal, se calculó la raíz del cuadrado medio del error (RMSE) entre el rendimiento observado y simulado, como la raíz cuadrada de la sumatoria de las diferencias al cuadrado sobre el número de observaciones; y el porcentaje de error (EE%) como el cociente entre el RMSE y el rendimiento observado promedio.

RESULTADOS Y DISCUSIÓN
Validación del modelo
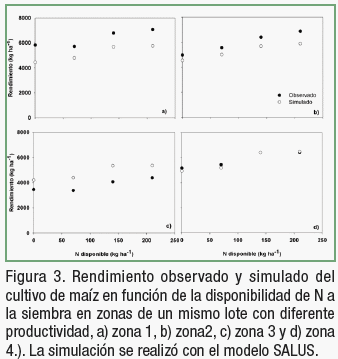
El modelo simuló adecuadamente el rendimiento del cultivo de maíz (RMSE=1169 kg ha-1; EE=14%, r2=0.82) (Figura 2), arrojando resultados similares en la performance del modelo a los obtenidos por Basso et al. (2011) al validarlo para simular la respuesta a N del cultivo de trigo. El modelo mostró sensibilidad a los cambios en las zonas de manejo, así como a las diferentes disponibilidades de N simuladas (Figura 3).
Dardanelli (2002) reportó similares resultados al simular con CERES-Maize distintas dosis de fertilización nitrogenada para sectores diferenciados de un lote (loma, media-loma y bajo) hallando que la magnitud de las respuestas decrece desde la condición más favorable (bajo), hacia la menos favorable (loma). En la zona 1 se observó una leve subestimación del rendimiento, de todas maneras la tendencia fue similar a la observada (Figura 3a).
En la zona 3, se observó una leve sobreestimación del rendimiento del cultivo de maíz (Figura 3c). Tanto en la zona 2 como en la 4 el modelo simuló la respuesta del rendimiento de maíz con mayor precisión (Figura 3b y 3d). Estos resultados son similares a los reportados por Basso et al. (2011) quien simuló la respuesta de trigo en tres zonas de alto, medio y bajo potencial de rendimiento.
Simulación de la respuesta a la fertilización nitrogenada en maíz a largo plazo En general, los testigos (0N) presentaron rendimientos más estables (CV 20-22%) y menores que los rendimientos simulados con las diferentes disponibilidades de fertilización por zonas variando entre 3500 y 4050 kg ha-1. El rendimiento simulado con 70 kg N ha-1 fue levemente más variable que el testigo (CV 21-24%) con valores entre 4300 y 5500 kg ha-1. La disponibilidad de 140 kg N ha-1 presentó rendimientos más variables (CV 22-27%) y mayores, entre 6000 y 7200 kg ha-1. El rendimiento obtenido con 210 kg N ha-1 en general fue mayor y mostró una mayor variabilidad (24-29%) en las 4 zonas evaluadas, con un rango entre 6500 y 8071 kg ha-1. En general, los menores rendimientos se obtuvieron en la zona 3 y los mayores en la zona 4, mientras que en las zonas 1 y 2 se obtuvieron rendimientos intermedios.
La respuesta simulada fue más estable para el nivel de N a la siembra de 70 kg ha-1, respecto a los otros niveles de N evaluados (Figura 4), con respuestas mayores a 750 kg ha-1 en las zonas 3 y 4 y de 1500 kg ha-1en las zonas 1 y 2 en el 50% de los años (Figura 4 a). En el nivel de N disponible de 140 kg ha-1 la respuesta fue más variable evidenciándose algunas diferencias entre zonas (Figura 4 b), en el 50% de los años es esperable que la respuesta sea mayor a 1000, 1500 y 1700 kg ha-1, en las zonas 2, 1 y 3, y 4, respectivamente.
La variabilidad de la respuesta fue mayor con el nivel de N disponible a la siembra de 210 kg ha-1 (Figura 4 c) y las diferencias entre zonas más marcadas, especialmente en el 25% de los años con mayor respuesta. Al 50% de probabilidad de ocurrencia se observaron respuestas de 250 kg ha-1 en las zonas 1 y 3, y de 600 y 1250 kg ha-1, en las zonas 2 y cuatro, respectivamente.
Estos resultados indican que es esperable obtener respuesta a la fertilización en todas las zonas de manejo evaluadas, aunque la magnitud de la respuesta depende del potencial de la zona. Esto refuerza el concepto de que las dosis de N deberían ajustarse diferencialmente dentro de los lotes, tal como ya han reportado trabajos previos (Muschetti Piana et al., 2010; Melchiori et al., 2009; Albarenque et al., 2009; Dardanelli, 2002). El uso de dosis de N variables dentro de los lotes de producción no sólo tiene implicancias económicas por la mejora en la eficiencia de uso del insumo utilizado, sino también que es tiene importantes consecuencias sobre la reducción del impacto ambiental de la práctica tecnológica.

CONCLUSIONES
El modelo SALUS simuló adecuadamente el rendimiento del cultivo de maíz mostrando sensibilidad a los cambios en las zonas de manejo y a la disponibilidad de N. Los resultados obtenidos de la respuesta simulada del cultivo de maíz a la fertilización nitrogenada a largo plazo sugieren que sería conveniente el ajuste de dosis según zonas de manejo.
En consecuencia, el modelo SALUS se presenta como una herramienta promisoria para apoyar las decisiones en el ajuste de dosis de fertilización nitrogenada en el manejo por zonas de diferente potencial productivo.
BIBLIOGRAFÍA
- Albarenque, S.M, R.J.M. Melchiori, y O.P. Caviglia. 2009. Utilización del modelo ceres-maize para la optimización de insumos en el manejo por ambientes. En: Melchiori R., Caviglia O., Albarenque S. & A. Kemerer (Eds). Jornada Nacional de Agricultura de Precisión: Integrando tecnologías para una agricultura sustentable.. Basso, B., Tien-Yin Chou, ChihYuan Chien, y MeiLing Yeh. 2012. I-SALUS: new web based spatial systems for simulating crop yield and environmental impact. ICPA
- Basso, B., J.T. Ritchie, D. Cammarano, y L. Sartori. 2011. A strategic and tactical management approach to select optimal N fertilizer rates for wheat in a spatially variable field. Europ. J. Agronomy 35: 215– 222
- Basso, B. 2005. Digital terrain analysis: data source, resolution and applications for modeling physical processes in agroecosystems. Rivista Italiana di Agrometeorologia 5-14 (2)
- Dardanelli, J.L. 2002. Utilización de modelos de simulación para el manejo sitio-específico. Tercer Taller Internacional de Agricultura de Precisión del Cono Sur de América, Carlos Paz, Córdoba.
- Doerge, T.A. 1999. Management zone concepts. SSMG-2. En: Information Agriculture Conference, August 9-11, 1999, Stewart Center, Purdue, IN.
- Jones, C.A, y J.R. Kiniry. 1986. CERES-Maize: A Simulation Model of MaizeGrowth and Development. Texas A&M University Press, College Station,TX, USA, p. 194.
- Jones, J.W., G. Hoogenboom, C. Porter, K.J. Boote, W.D. Batchelor, L.A. Hunt; P. Wilkens, U. Singh, A. Gijsman, y J.T. Ritchie. 2003. The DSSAT cropping system model. Eur. J. Agron. v18, p. 235-265.
- Melchiori, R.J.M., S.M. Albarenque, G. Schulz, A.C. Kemerer, y D.J. Bedendo. 2009.Delimitación de zonas de manejo mediante relevamiento de suelos y herramientas informáticas. En: Melchiori, RJM; O Caviglia; SM Albarenque & AC Kemerer (Eds). Jornada Nacional de Agricultura de Precisión: Integrando tecnologías para una agricultura sustentable.
- Melchiori, R.J.M. 2007. Agricultura de precisión en Entre Ríos, aspectos relacionados con la sustentabilidad. En: Caviglia, OP; OF Paparotti & MC Sasal (Eds). Agricultura sustentable en Entre Ríos. p. 195-200.
- Miao, Y., D.J. Mulla, W.D. Batchelor, J.O. Paz, P.C. Robert, y M. Wiebers. 2006. Evaluating management zone optimal nitrogen rates with a crop growth model. Agron. J. v98, p. 545-553.
- Mulla, D.J., y J.S. Schepers. 1997. Key processes and properties for site-specific soil and crop management. En: The State of Site Specific Management for Agriculture. ASA-CSSA-SSSA. Madison WI. Ed: F.J. Pierce and E.J. Sadler. p. 1.
- Muschetti Piana, M.P., P.A. Cipriotti, H. Rimski- Korsakov, y S. Urricariet. 2010. En: Actas del XXII Congreso Argentino de la ciencia del Suelo, Rosario, Argentina.
- Pierce, F.J., y P. Nowak. 1999. Aspects of precision agriculture. In: D. Spark (Ed). Advance in Agronomy 67, Academic Press. p. 1-85.
- Rinaldi, M. 2004. Water availability at sowing and nitrogen management of durum wheat: a seasonal analysis with the CERES-Wheat model. Field Crops Res. v89, p. 27-37.
- Ritchie, J.T., y S. Otter. 1985. Description and performance of CERES-Wheat: a user-oriented wheat yield model. In: ARS Wheat Yield Project. ARS-38.Natl. Tech. Info. Serv., Springfield, MO, USA, pp. 159–175.
- Van Barneveld, G.W. 1972. Los suelos de la Estación Experimental I.N.T.A. Paraná. Plan Mapa de Suelos Provincia de Entre Ríos. Proyecto PNUD/FAO/INTA ARG/68/526. 50 p.
Contenido del evento:
Temas relacionados:
Mencionados en esta noticia:




Mostrar más
Recomendar
Comentar
Compartir
30 de octubre de 2015
hola buen dia German Lizarzaburu, te dejo el link de una pagina donde ellos ofrecen este software, bueno al menos en lo personal se me hace uno de los mejores que han salido al mercado, por su eficiencia.
( http://www.smart-fertilizer.com/es)
Recomendar
Responder
29 de octubre de 2015
El trabajo de investigación muy importante, permite simular y regular dosis en otras partes del mundo, me gustaría saber como consigo el software para aplicar en mi pais.
Saludos
Recomendar
Responder
28 de octubre de 2015
HOLA BUEN DIA A TODOS. CADA COMENTARIO SOBRE LA PREGUNTA QUE REALIZA EL SR. JORGE ROMERO, SOBRE LA RECOMENDACION DE QUE EN CANTIDAD DE FERTILIZANTES, SE DEBE APLICAR AL MAIZ, Y TANTO EL MOMENTO CRUCIAL, LA RESPUESTAS QUE LEI, TODAS EN PARTE LLEVAN AL CORRECTO PUNTO DE LA PREGUNTA DEL SR. JORGE, PERO HAY ALGO QUE SE TIENE QUE TOMAR EN CUANTA QUE ES LA LEY DEL MINIMO DE LIEBING, QUE TODOS EN EL CASO DE LOS QUE NOS DEDICAMOS EN LO PROFESIONAL A LA AGRICULTURA CONOCEMOS, Y QUE DICE QUE CON UN SOLO ELEMENTOS QUE LOS QUE NECESITA CUALQUIER CULTIVO, Y AUNQUE TODOS LOS DEMAS ESTEN LAS CANTIDADES ADECUADAS, ESTE AFECTA EN GRAN MEDIDA EN EL DESARROLLO Y PRODUCCION O RENDIMIENTO DEL CULTIVO, QUE TAMBIEN ES FACTOR DE ATENCION, PORQUE TENDRIA QUE HACERME LA PREGUNTA CUANTO QUIERO PRODUCIR POR HECTAREA. MIL GRACIAS. (CONOZCO A UN CATEDRATICO QUE SE DEDICABA A DAR CONFERENCIAS PRECISAMANTE DEL CULTIVO DEL MAIZ, Y SIEMPRE AL COMENZAR SU CHARLA, AL PUBLICO ASISTENTE LE HACIA UNA PREGUNTA, ¿ CONOCEN UDS. AL MAIZ?, CLARO QUE MUCHOS DE LOS ASISITENTES CONTESTABAN QUE SI, Y AL FINAL DEL DEBATE DE ESTA PREGUNTA EL LES RESPONDIA. ! SRES. YO TENGO MAS DE CUARENTA AÑOS ESTUDIANDO AL MAIZ Y TODAVIA NO LO CONOZCO¡...
Recomendar
Responder


Efecto de la fertilización nitrogenada sobre el contenido en grasa del grano de colza
Enlace recomendado
28 de octubre de 2015
Hola estimado colegas y demás participante. siempre que queramos sembrar algún cultivo no olvidemos los análisis de suelo que son de mucha importancia para conocer que tenemos deficiencia o exceso de nutrientes en nuestro suelo y así poder ahorrar en el costo de producción.
Recomendar
Responder
Recomendar
Responder
Recomendar
Responder
26 de octubre de 2015
Mande usted una muestra de suelo a un buen laboratorio de suelos en su zona y cuando tenga los resultados hagamelos llegar y con todo gusto le podre dar una recomendación de los fertilizantes, cantidades y época para aplicarlos. Sin el análisis es imposible hacerlo
Recomendar
Responder
26 de octubre de 2015
Saludos cordiales.
Por favor necesito saber urgentemente, cual es la necesidad de fertilizante que necesita el maiz, N-P-K-Ca-Mg-otros para suelos rojos ricos en hierro y magnesio, de ph acidos.
Y cuales son las epocas propicias para aplicar los fertilizantes, de cuando a cuando o hasta que etapa fenologica
Recomendar
Responder
25 de octubre de 2015
Muy acertado el comentario, pues una adecuada fertilizacion , no significa una enorme cantidad de fertilizante innecesario, ni que todo tiene que ser supersoluble, quimico y super concentrado, simplemente proporcionarle a la planta su necesidad, y puede ser por diferentes vias y no excluyo la organica, pero partiendo del suelo de su condicion , de su salud y su contenido, contraponiendolo a la extraccion de cada cultivo y variedad. Cuando esto se maneje bien, tambien disminuyen los riesgos de plagas y se obtendran mejores rendimientos
Recomendar
Responder
25 de octubre de 2015
Sin duda la falta de la práctica del análisis de suelo es el factor más limitarte en la producción de maíz no sólo en México sino un otros países, el uso de cantidades arbitrarias de fertilizantes tanto en cantidad como en calidad, es en muchos casos en los que se convierte en el factor limitante. Si en nuestra zona (Fresnillo, Zacatecas, México) se están obteniendo frecuentemente producciones en riego de 15 o más toneladas por hectárea y ocasionales de (18 toneladas) es por qué los nuevos híbridos tienen un potencial de producción mayor a estos rendimientos que son resultado de una correcta fertilización, riego y manejo agronómico, seguramente en cualquier lugar se pueden obtener resultados similares cuando el manejo sea el óptimo.
Recomendar
Responder


Efecto de la fertilización nitrogenada sobre el contenido en grasa del grano de colza
Enlace recomendado

¿Quieres comentar sobre otro tema? Crea una nueva publicación para dialogar con expertos de la comunidad.













