Modelaje de los requerimientos de metionina + cistina para aves de postura en crecimiento

El uso de aminoácidos en la nutrición avícola se ha venido desarrollado y ha consolidado conceptos a lo largo del tiempo, desarrollo que se ha visto favorecido con el uso del modelaje. La elaboración y validación de modelos biológicos en sus diferentes formas (estáticos, dinámicos, empíricos, mecanicista, determinista y estocástico), han contribuido a integrar nuevos conceptos y facilitar la interpretación de las relaciones entre fenómenos biológicos y han sugerido nuevos temas de investigación.

El modelaje mecanicista explica mejor los fenómenos que participan en la respuesta animal. Con respecto al uso de aminoácidos en la ración, estos modelos ayudan a entender mejor la relación entre mantenimiento, crecimiento, (depósito de proteína) y eficacia en la utilización de aminoácidos para calcular sus requerimientos. De esta forma, ahora se ha aceptado y comprendido la teoría propuesta por Emmans (1981; 1997) de que los requerimientos se determinan en función del potencial genético de crecimiento de las aves. Una vez que podemos comprender que el depósito diario de aminoácidos en el cuerpo sin plumas y en las plumas gracias a la primera derivación de la ecuación de crecimiento de Gompertz, relacionado con la eficiencia de dicho depósito, se estima el requerimiento líquido para alcanzar el máximo depósito de proteína (DP_max) o rendimiento animal. Al tratarse de los aminoácidos en la nutrición es necesario tomar en cuenta sólo el metabolismo proteico para estimar el requerimiento de mantenimiento que, por definición, anula el efecto de los diferentes constituyentes tisulares del cuerpo. Esto se debe a que cada genotipo tiene su nivel máximo de peso proteico y DP_max. y, estos conceptos no sufren la influencia del aumento en el consumo de energía, lo que no ocurre con el tejido adiposo (Emmans, 1981; Emmans y Kyriazakis, 1997). Con base en la información expuesta y debido a la escasez de datos relacionados con el modelaje, el objetico del presente estudio fue calcular los parámetros de un modelo para predecir los requerimientos de metionina + cistina, con base en el metabolismo proteico para pollas de reemplazo para postura.

La presente investigación se realizó en la Universidad del Estado de Sao Paulo (UNESP), Campus Jaboticabal, para estimar los parámetros del modelo y predecir los requerimientos de metionina + cistina, con base en el metabolismo proteico de las pollas de reemplazo para postura de 1 a 18 semanas de edad. El modelo adoptado sigue la estructura propuesta por Martin et al. (1994):

N. del T: A continuación presentamos la ecuación tal como aparece en el original en portugués

EAA_mg/ave/dia = [a . dPC/dt + b . dPP/dt]/k + [_MCORPO_met+cis + _MPENAS_met+cis];

Que traducido al español sería:

EAA_mg/ave/día = [a . dPC/dt + b . dPP/dt]/k + [_MCUERPO_met+cis + _MPLUMAS_met+cis];

en donde: EAA = requerimiento de metionina + cistina (mg/ave/día); a = contenido de metionina + cistina en la proteína del cuerpo sin plumas; b = contenido de metionina + cistina en la proteína de la pluma; dPC/dt = depósito de proteína corporal obtenido mediante la primera derivación de la ecuación de Gompertz; dPP/dt = depósito de proteína en la pluma obtenido mediante la primera derivación de la ecuación de Gompertz; k = eficiencia en la utilización de metionina + cistina; _MCORPO_met+cis = requerimiento de metionina + cistina para el mantenimiento de la proteína corporal; _MPENAS_met+cis = requerimiento de metionina + cistina para mantenimiento de la proteína de la pluma. Los parámetros a y b se obtuvieron de acuerdo con Emmans (1989).

Se obtuvieron los parámetros de crecimientos de tres estirpes de aves en trabajos anteriores realizados en la UNESP-Jaboticabal, con base en la ecuación de Gompertz: PP_t = PP_m exp [ - exp (( ln ( - lnPP₀/PP_m)) - (B_PP.t))] para el crecimiento del cuerpo sin plumas y de las plumas; la primera derivación de esta ecuación proporciona la ganancia o depósito, en donde dPC/dt (cuerpo) y  dPP/dt (plumas) se obtuvieron por medio de dPC/dt y dPP/dt = PPt.B_PP.ln(1/(PP_m/PPt)), en donde PP_t = peso proteico al tiempo t, aplicado al cuerpo sin plumas y a las plumas; PP_m = peso proteico a la madurez aplicado al cuerpo sin plumas y a las plumas; PP₀ = peso proteico al tiempo cero o al nacimiento, aplicado al cuerpo sin plumas y a las plumas; B_PP = tasa de maduración de la proteína o crecimiento relativo en el punto de inflexión, por día, aplicado al cuerpo sin plumas y a las plumas.

La eficiencia de utilización de metionina + cistina (k) se obtuvo en tres ensayos con pollas de reemplazo Dekalb White de 1 a 18 semanas (iniciación, cría y recría). Considerando la ganancia proteica (cuerpo + plumas) y la composición de metionina + cistina en la proteína corporal (cuerpo + plumas) de las aves en las tres fases citadas, se obtuvieron los depósitos de metionina + cistina. Por medio de la regresión lineal entre el depósito (Y) y el consumo (X) para depósito (metionina + cistina ingerida - metionina + cistina para mantenimiento) se calculó la eficacia en la utilización de los aminoácido, coeficiente lineal.

El coeficiente de mantenimiento se calculó en experimentos anteriores con gallos adultos, realizados en la UNESP, Jaboticabal siendo: _MCORPO_met+cis (_MCUERPO_met+cis) = 87.26 mg de metionina + cistina/unidad de PP_m^0.73/día. Los requerimientos se expresaron con base en el concepto propuesto por Emmans (1987), donde _MCORPO_met+cis (_MCUERPO_met+cis) = Met+Cis_m.PP_m^0.73. PPt/PP_m. donde Met+Cis_m es el requerimiento de metionina + cistina (mg/día); PP_m, PP_t e PP_m = los describimos ya en el texto que antecede; y la relación entre PP_t/PP_m es el u o grado de madurez de la proteína corporal, factor que corrige los cambios en función del tiempo. El requerimiento de _MPENAS_met+cis (_MPLUMAS_met+cis) se consideró equivalente a la tasa de pérdida de plumas del cuerpo. La pérdida diaria de plumas se ha sugerido como 0.01*PP_penast*b (Emmans, 1989), el equivalente de esta cantidad se debe reponer todos los días; en donde 0.01 es la tasa de pérdida de plumas del cuerpo, en g/día; PP_penast, es el peso proteico de las plumas al tiempo t; b, fue descrito ya con anterioridad. Con base en estos parámetros se elaboró el modelo para estimar los requerimientos de metionina + cistina digestibles para tres genotipo, Hy Line, Hisex y Dekalb en las fases de iniciación, cría y recría.

El modelo elaborado de acuerdo con la teoría propuesta por Emmans (1981; 1997) para predecir los requerimientos de metionina + cistina fundamentados en el metabolismo proteico para pollas de postura, se presenta a continuación:

N. del T.: tal como aparece en el documento original en portugués:

Met+Cis_mg/ave/dia = [36 . dPC/dt + 76 . dPP/dt]/0.794 + [87.26 . PP_m^0.73. u + 0.01.PPpenast*76];

que en español sería:

Met+Cis_mg/ave/día = [36 . dPC/dt + 76 . dPP/dt]/0.794 + [87.26 . PP_m^0.73. u + 0.01.PPplumast*76];

En donde Met+Cis es el requerimiento de metionina + cistina (mg/ave/día). Los valores 36 y 72 corresponden al contenido de metionina + cistina en la proteína del cuerpo sin plumas y en las plumas, respectivamente. Los parámetros dPC/dt y dPP/dt, son los depósitos de proteína corporal y de proteína de la pluma obtenidos mediante la primera derivación de la ecuación de Gompertz. La eficiencia en la utilización de metionina + cistina que se determinó fue 79.4%. El valor de 87.26 es el requerimiento de metionina + cistina para el mantenimiento de la proteína corporal, y 0.01 es la tasa diaria de pérdida de plumas en el ave.

El modelo fue estructurado por medio de ecuaciones simples compuestas de parámetros con significado biológico, lo que facilita el entendimiento del metabolismo proteico del ave (Martin et al., 1994). Para utilizar este modelo basta tan solo conocer la composición corporal de las aves de un determinado genotipo y la descripción de su crecimiento.

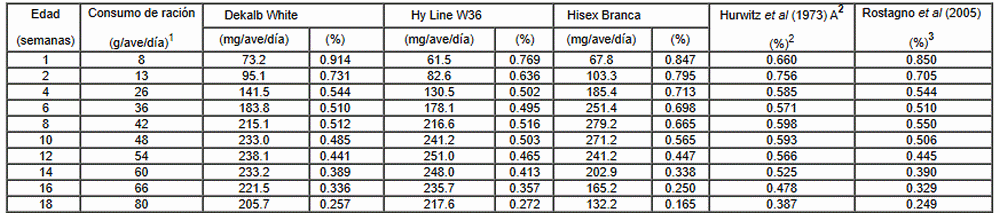
Con base en los parámetros presentados en el Cuadro 1 se simuló el crecimiento de tres estirpes y se aplicó el modelos para calcular los requerimientos de metionina + cistina de las tres estirpes. Los resultados obtenidos con el modelo elaborado se presentan en el Cuadro 2. Las diferencias observadas entre los genotipos son concernientes a las diferencias en los parámetros descriptores del crecimiento del tejido proteico en las aves. Estas diferencias pueden implicar un mayor o menor depósito de proteína (PP_m) así como precocidad en el desarrollo (B_pp). Esto implica decir que las estirpes se deben evaluar nuevamente para utilizar estos parámetros, que sufren modificaciones constantes a causa de la intensa selección genética. Específicamente para la estirpe Dekalb White, los modelos de crecimiento elaborados por Hurwitz y Bornstein (1973) y Rostagno et al. (2005) se simularon y los resultados se presentan en el Cuadro 2.

Se observó el modelo propuesto describió el requerimiento diario de metionina + cistina digestibles de manera coherente, cuando se compararon la información disponible en la literatura (Hurwitz y Bornstein, 1973; Rostagno et al., 2005).

Los modelos de Hurwitz y Bornstein (1973) y Rostagno et al. (2005) presentan diferencias que pueden ser atribuidas a los conceptos empleados en la estructura paramétrica de los modelos. El mantenimiento utilizado por Hurwitz y Bornstein (1973) trata de forma lineal la demanda de aminoácido en los sistemas celulares, pero el metabolismo no aumenta proporcionalmente al peso vivo del animal. Bonato (2010) verificó que la equivalencia utilizada por estos autores (107.1 mg/Kg) en unidad de peso metabólico proteico de 449 mg, PP_m^0.73.u /día, cerca de 5.7 veces más aminoácido se destina al mantenimiento, en comparación con el coeficiente utilizado en el modelo propuesto en el presente trabajo (87.26 mg PP_m^0.73.u /día).

Cuadro 1. Parámetros de las ecuaciones de Gompertz para peso proteico en el cuerpo sin plumas (PPC) y peso de la proteína de las plumas (PPP) de las diferentes estirpes de aves^s

Cuadro 2. Estimados de los requerimientos de metionina + cistina digestibles en pollas de reemplazo para postura

De manera similar al presente trabajo, los requerimientos de crecimiento de Hurwitz y Bornstein (1973) se obtuvieron tomando como referencia la proteína ideal, y la composición de aminoácidos de la canal del ave. De esta manera, a medida que aumenta el depósito de aminoácidos en la canal con el tiempo, aumenta también su requerimiento.

El uso del peso metabólico para determinar los requerimientos de mantenimiento se prevé en el modelo propuesto Rostagno et al. (2005) y el parámetro para los requerimientos de crecimiento considera la ganancia de peso del ave, que puede sufrir variaciones en su composición tisular, (proporción grada/proteína) en función del consumo de energía (Emmans, 1981; Emmans y Kyriazakis, 1997). Por otro lado, el modelo propuesto en este trabajo expresa los requerimientos de mantenimiento por unidad de mantenimiento y para el crecimiento, tomando en consideración el depósito de proteína tanto en el cuerpo como en las plumas.

Bajo las condiciones comparadas se observa que hasta la sexta semana de edad existe semejanza entre los estimados de los modelos. Sin embargo, a partir de esta edad se observan diferencias conceptuales entre los modelos. Los requerimientos publicados por Rostagno et al. (2005) son mayores hasta la semana 13 de vida, y después de esta edad, en función de la reducción de la ganancia de peso se observa una disminución en el requerimiento. Es necesario señalar que, en condiciones de campo, a partir de esta edad la ganancia en grasa puede asumir una gran parte de la participación en el estimado de los requerimientos, toda vez que el ave se encuentra en un estado fisiológico próximo a alcanzar su DP_max.

El modelo propuesto en este estudio describió de manera congruente los requerimientos de metionina + cistina digestibles considerando las modificaciones fisiológicas del ave en función de su edad. Su entendimiento contribuye a conocer el metabolismo proteico y a economizar en los programas nutricionales.

Bonato MA. 2010. Exigências de metionina + cistina e treonina para manutenção de aves. Dissertação de Mestrado em Zootecnia. Universidade Estadual Paulista, Faculdade de Ciências Agrárias e Veterinárias, 68f.

Emmans GC. 1981. A model of the growth and feed intake of ad-libitum fed animals, particularly poultry, in: Hillyer GM, Whittemore CT, Gunn RG (Eds) Computers in Animal Production, pp. 103-110, Animal Production, Occasional Publication No. 5 (London).

Emmans GC. 1989. The growth of turkeys, in: Nixey C & Grey TC (Eds) Recent Advances in Turkey Science, pp. 135-166 (London, Butterworths).

Emmans GC. 1997. A method to predict the food intake of domestic animals from birth to maturity as a function of time. J. Theor. Biol. 186:189-199.

Emmans GC & Kyriazakis I. 1997. Models of pig growth: problems and proposed solutions. Livest. Prod. Sci. 5:119-129.

Hurwitz S & Bornstein S. 1973. The protein and amino acid requirements of laying hens: suggested models for calculation. Poultry Sci. 52:1124-1134.

Martin PA, Bradford GD, Gous RM. 1994. A formal method of determining the dietary amino acid requirements of laying type pullets during their growing periods. Brit. Poultry Sci. 35:709-724.

Rostagno HS, Albino LFT, Donzele JL, Gomes PC, Oliveira RFM, Lopes DC, Ferreira AS, Barreto SLT. 2005. Tabelas brasileiras para aves e suínos: composição de alimentos e exigências nutricionais. 2. ed. Viçosa, MG: Departamento de Zootecnia, Universidade Federal de Viçosa.