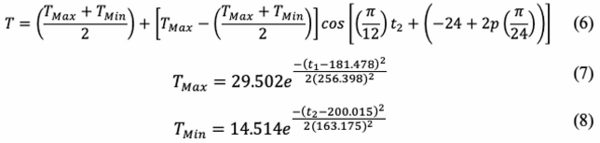Introducción
Las pérdidas postcosecha asociadas con el almacenamiento de granos atribuibles a condiciones climatológicas y de manejo adversas, destacan la necesidad imperativa de realizar estudios y análisis sobre el almacenamiento de granos. El almacenamiento de granos implica la preservación de la calidad inicial de aquellos mediante el control de las condiciones ambientales del almacén y la minimización de la in uencia de los agentes que causan deterioros, con el n de reducir los efectos que una excesiva oferta postcosecha produciría en los precios. Los granos representan la principal fuente de alimento tanto para la población humana como para el ganado, siendo fundamentales en la dieta, incluyendo los granos básicos como el maíz, el frijol, el arroz y el trigo, los cuales son esenciales para la alimentación y las prácticas culturales del país.
El metabolismo del grano (es un tejido vivo), la humedad del grano, la humedad relativa del aire (tanto intersticial como ambiental) y las condiciones climáticas son considerados los factores más importantes a identi car y controlar para preservar la calidad e inocuidad del grano durante su almacenamiento. Estos factores tienen una interrelación mutua, si la humedad aumenta, el calor de respiración también, donde haya puntos calientes y húmedos es posible el crecimiento de hongos y migración de plagas lo que, en consecuencia, favorece un microambiente idóneo para la descomposición del grano. También, los gradientes de temperatura causan migración de la humedad y las temperaturas se ven afectadas por fuentes de calor internas y externas [1].
Por otro lado, es evidente que temperaturas más bajas previenen el desarrollo de insectos, hongos y otras plagas que, también se pueden controlar reduciendo la actividad de agua [2]. Por esta razón se deben atender estos problemas de almacenamiento desde el punto científico (estableciendo las ecuaciones que gobiernan los fenómenos que se han comentado previamente), para optimizar los procesos actuales de almacenamiento.
Similarmente, el análisis tridimensional del fenómeno de convección natural también ha evolucionado, varios autores [3] han comentado que en este rubro se analizan dos clases generales, uno en el que se tiene una cavidad con todas sus paredes aisladas y calentada de la parte inferior; la segunda donde se tienen dos paredes verticales opuestas a diferentes temperaturas y el resto de las paredes aisladas. En estas concepciones generales se han realizado múltiples estudios, la importancia de este trabajo recae en que se consideró un cuerpo dentro del espacio con generación de calor y el efecto que este podría provocar en los patrones de flujo dentro de la cavidad.
Anteriormente se han encontrado comparaciones del uso de diferentes herramientas de solución que aborden el problema de la convección natural en una cavidad tridimensional [4]. Este tipo de estudios muestran cómo se ha evolucionado en las diferentes técnicas y tecnologías que pueden ayudar a la solución de este problema, de esta forma se abrió el camino para el estudio de medios bifásicos con generación de calor, como es el caso de los medios porosos. El análisis de la convección natural en un medio poroso de un caso práctico de tres dimensiones es el almacenamiento de granos, se puede justificar un diseño tridimensional de este sistema debido a la influencia del sol en una de las caras del silo y su variabilidad con respecto al tiempo debido al ciclo diurno-nocturno y al ciclo estacional junto con el gradiente de temperatura en la super cie exterior del silo.
Existen estudios realizados para medios porosos con consideraciones de variación azimutal de la temperatura [5], [6] donde se tienen estudios completos y a detalle en dos dimensiones del fenómeno en medios porosos y se puede encontrar una amplia referencia en el Manual de Medio Poroso [7] y en otros trabajos [8], [9]. Los modelos matemáticos son la base racional para el diseño de múltiples procesos y la tecnología de cualquier tipo, se ha ampliado su aplicación a todos los campos de la ciencia e incluso es fundamental en la mayoría de los procesos; es indispensable en la optimización y desarrollo de tecnología más eficiente y una de las áreas que no han salido de su amplio espectro es el almacenamiento de grano donde juega un papel muy importante, ya que debido a estos modelos se puede predecir el comportamiento de diversos factores que influyen en el deterioro de los granos.
Antecedentes
Almacenamiento de granos en silos
En la conservación de alimentos el estudio de los fenómenos de transporte para determinar el comportamiento de un producto durante su almacenamiento es un asunto de análisis continuo, de esos estudios se toman pautas de diseño estructural, de empaques, de metodologías de almacenamiento, entre otros. Dentro de la gama de productos que se almacenan siempre vienen involucrados productos que tienen un comportamiento como medio poroso, como es el caso del estudio de enfriamiento de papa [10], donde se realizó un experimento real y se modeló el comportamiento matemático, de esta forma se observó que la modelación matemática de productos para su conservación es factible porque es precisa en las predicciones.
Los hongos, por otra parte, tienen necesidades especiales diferentes a las de los insectos, por lo tanto, necesitan ser modelados de forma diferente, aunque en algunos estudios se apoyan con datos experimentales y tratan de calcular valores más bien generales [11]. Otros trabajos utilizan las ecuaciones de momentum, calor y masa para modelar el comportamiento del grano en tres dimensiones [12], este trabajo es bastante completo en cuestión de matemáticas aun cuando no considera el equilibrio termodinámico entre la humedad del grano y la humedad relativa del aire (relacionada con la actividad acuosa a local del grano). En este trabajo se resuelve el sistema de ecuaciones con el método del falso transitorio en la ecuación de momentum, por lo tanto, no utiliza la vorticidad, tiene la desventaja de no presentar la dinámica del problema, además tiene condiciones de frontera constantes.
Se han realizado investigaciones con el objetivo de tomar en consideración los efectos ambientales, el espacio de cabeza y los ujos de calor dentro del silo, pero el inconveniente es que maneja el sistema como si fuera exclusivamente conducción [13], por lo tanto, pierde el efecto provocado por el movimiento del ujo de aire y las interacciones internas que contiene. En otra investigación se tomó como patrón un modelo de tres dimensiones de trabajos previos [14] [15], pero los modelos propuestos solamente consideraron la conducción de calor, igualmente del modelo de [16] trató de simular con un software comercial el fenómeno de almacenamiento de granos en silos, considerando la pared de lámina de metal y otras características más cercanas a la física real del sistema, pero siguió utilizando un modelo exclusivamente de conducción.
Cabe comentar que se han formulado modelos tratando de integrar el efecto ambiental utilizando las ecuaciones de momentum, calor y masa; algunos se basan en datos que deben estar siendo monitoreados continuamente [17] mientras que otros, de manera más práctica, pero un poco menos preciso, utilizan un modelo donde se determine el efecto de las variaciones ambientales de forma global utilizando pocos datos [8]. Se puede observar la carencia de modelos matemáticos que consideren el medio poroso en el almacenamiento de granos con los efectos de convección natural y los efectos ambientales. Otra metodología usada frecuentemente es almacenar una base de datos de temperaturas tomando lecturas de temperaturas mediante el uso de termopares, esto con el objetivo de observar las uctuaciones de calor en el silo, con este método se han observado fluctuaciones de calor el espacio de cabeza del silo y menor en el grano, detectando la zona con mayor gradiente de temperatura en el centro del silo, cerca de la supercie [18].
Además, varios trabajos analizaron el fenómeno de transferencia de calor y masa en silos adaptado a un enfoque en tres dimensiones utilizando el método de diferencias nitas para resolver el problema, esto con el n de predecir los tiempos de secado y de formación de microorganismos en el silo [19], [20]. También se han propuesto varios modelos basados en la dinámica computacional de uidos para resolver problemas que se basan en la descripción de los per les de transferencia de masa y calor en bolsas de silo [21]. Otros trabajos se han enfocado en el estudio de la distribución de humedad y el efecto de la convección natural en los per les de transferencia de masa y energía en silos metálicos [22].
Diferentes modelos proponen un enfoque en dos dimensiones aplicando el método de elemento nito aplicado a la predicción de los per les de distribución de calor y temperatura en la soya almacenada en silos. Utilizando condiciones iniciales que simulan el inicio de las estaciones, lograron predecir que, en primavera la convección natural del silo aumenta, disminuyendo el contenido de humedad, siendo la permeabilidad el factor que más afecta el transporte [23]. De la misma manera se han hecho estudios numéricos, que posteriormente se veri caron con resultados experimentales, sobre la convección natural en tres dimensiones de silos y un almacén de grano tipo bodega. Para acercarse a la realidad se han añadido condiciones de frontera de tipo ambiental y modelos de radiación para calcular la temperatura de la super cie [24]. Se llegó a la conclusión de que el grano cerca de la pared del silo tiene una transferencia de calor más rápida, sin embargo, también se ve afectada por la temperatura interna del mismo.
Al respecto, la Figura 1 ilustra la complejidad del efecto acoplado de la temperatura ambiental y de la radiación solar, ya que la fotografía infrarroja del silo de estudio muestra un gradiente de temperaturas sobre la super cie exterior del silo, lo que va a determinar las temperaturas que se mani esten en la masa del grano, por lo que es importante el uso de modelos para la predicción de patrones de ujo, isotermas e isolíneas de humedad [9].
 Figura 1. Silo comercial de almacenamiento de maíz y su imagen térmica correspondiente. Fuente: Trabajo de campo
Figura 1. Silo comercial de almacenamiento de maíz y su imagen térmica correspondiente. Fuente: Trabajo de campoEl objetivo del almacenamiento de granos es su conservación mediante el control de los factores que afectan su deterioro, como la humedad, la temperatura y la radiación solar. Los modelos se utilizan para poder predecir el comportamiento y el efecto de estos factores, como se ha descrito en esta sección, varios autores han hecho hallazgos importantes ya sea utilizando modelos o haciendo investigación experimental. Dado que el clima es un factor de gran importancia, se ha intentado incorporar a estos modelos, sin embargo, es difícil encontrar un algoritmo completamente preciso para predecir la temperatura ambiental. Otra di cultad a la que se han enfrentado los investigadores es encontrar el modelo correcto de los almacenes de grano ya que la mayoría son investigaciones que se manejan usando modelos en dos dimensiones. Sin embargo, el problema completo en tres dimensiones sigue siendo un caso de estudio vigente. Por lo tanto, el objetivo de este trabajo es incrementar el nivel de so sticación de la modelación matemática que incluyan modelos climáticos y el efecto de la radiación solar, con el n de acercarse paulatinamente a la física real del problema.
Por último, es importante comentar que medir la temperatura o la humedad en el interior de un silo puede conllevar ciertos riegos. Algunos posibles accidentes o peligros que una persona podría enfrentar al realizar estas mediciones o al colocar los termopares o sensores correspondientes incluyen: Atmosfera tóxica o falta de oxígeno, colapso de granos, polvo y partículas en suspensión, caídas y atrapamientos, por lo que la modelación matemática y simulación de la dinámica del almacenamiento se convierta en una herramienta para el diseño e ciente de estrategias de conservación.
-Metodología
Fundamentos matemáticos
 Figura 2. Dominio computacional y geométrico 2-D del problema
Figura 2. Dominio computacional y geométrico 2-D del problemaEl problema de estudio consistió en un silo cilíndrico a escala industrial con una altura L y un radio R (ver Figura 2). Para las simulaciones se considera el grano como un medio poroso isotrópico saturado con un uido newtoniano (aire). Los granos presentan valores de permeabilidad K del orden de 10 resultando el número de Darcy del orden de 10 . Para obtener el modelo correspondiente al sistema geométrico en cuestión se hicieron las siguientes consideraciones:
Medio efectivo, isotrópico con propiedades constantes donde la viscosidad y la densidad corresponden al uido y la conductividad térmica es la efectiva del medio poroso. Además, se utiliza la aproximación de Boussinesq para calor ρ = ρ [1-β(T-T )] que considera constante la densidad, excepto en el término de fuerzas volumétricas [9]. Con estas restricciones, y utilizando variables adimensionales se obtiene el modelo matemático, que representa los mecanismos de transporte que ocurren en el interior del silo expresadas en notación vectorial:
Condiciones de frontera con condiciones climáticas
Las condiciones de frontera de temperatura incluyen el suelo aislado (piso del silo), que es un sistema asimétrico, y las temperaturas de la pared lateral y superior, que están indicadas por los límites climáticos determinados por un modelo basado en el reporte de Carrera-Rodríguez et al. (2011) y publicado previamente [27]. Para evitar aumentar la di cultad de la solución, este modelo para predecir la temperatura ambiente usa un número reducido de parámetros como la temperatura promedio, los tiempos, la humedad y la radiación. Usando el menor número de parámetros se evitará la necesidad de adquirir una gran cantidad de equipos y simpli cará el modelo.
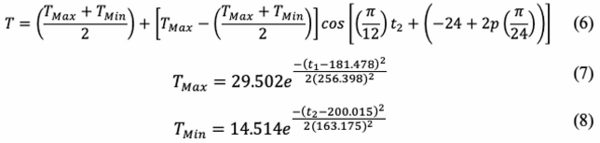
Este modelo requiere 3 constantes para calcular la temperatura máxima y la temperatura mínima que se puede obtener a través de regresión no lineal contra datos experimentales para todo el año; en este caso, los datos se obtuvieron de Tutiempo.net S.L. Página web, que recopila datos de centros meteorológicos europeos con bases de datos de todo el mundo. Los datos son de acceso público. Las ecuaciones 6 a 8 predicen la temperatura ambiental (°C) en cualquier momento del día y estación en el transcurso del año. Usando la de nición del número de Fourier Fo= ta/R2 y reacomodando los términos se obtiene la ecuación 10:
La ecuación nal que predice la temperatura adimensional en la frontera es:
Este modelo se obtuvo a partir de los datos estadísticos registrados en Celaya, Guanajuato, México, con una longitud de 100 ° 48ʹ W, latitud 20 ° 31ʹ N y altitud 1750 m. Celaya es parte de una región agrícola conocida como “Bajío”. Se eligió este modelo de temperatura ambiental como función de tiempo porque es fácilmente ajustable para la incorporación posterior de radiación solar, velocidad del viento y otros factores climáticos.
Condiciones de frontera de radiación
El silo también está expuesto a la radiación solar que incide sobre la super cie y aumenta la temperatura en la pared y el techo del silo, este aumento puede llegar a ser muy alto dependiendo de la hora del día [28], para considerar estos efectos en el modelo, es necesario disponer de ecuaciones que predigan la irradiación de acuerdo con la hora del día. Du e y Beckham recopilan las ecuaciones que describen la cantidad de radiación que recibe un cuerpo [29]:
Para predecir la temperatura super cial se utilizó la ecuación (11), que involucra la temperatura ambiental y propiedades propias de la super cie, como la absorbancia y el ángulo de incidencia, este modelo se acopló junto con el de la temperatura ambiental en las condiciones de frontera.
Donde es la absorbancia de la super cie, es el Angulo de incidencia, es la insolación y es la constante de Stefan-Boltzman.
Método de solución
La estrategia global para resolver el sistema de ecuaciones diferenciales parciales (EDP) radica en reducirlas a una o más ecuaciones diferenciales ordinarias (EDO) o a un conjunto de ecuaciones algebraicas y la solución de estos sistemas se logra aplicando métodos numéricos.
Colocación ortogonal
El método de Colocación Ortogonal para la solución de ecuaciones diferenciales con valores en la frontera se aplica para resolver múltiples problemas, principalmente enfocados a ingeniería química [30], y se ha usado más tarde para resolver diferentes problemas [30], [31], [32], [33]. Colocación Ortogonal (CO) permite convertir ecuaciones diferenciales ordinarias a ecuaciones algebraicas y ecuaciones diferenciales parciales del tipo parabólico, a ecuaciones diferenciales ordinarias con valores iníciales [33]. Para el método de CO, los puntos donde el residuo se hace cero corresponden a las raíces de polinomios ortogonales como los de Legendre, Jacobi, Hermite, Laguerre, entre otros. Estos se emplean como soluciones de prueba, por lo que el error disminuye más rápido cuando se incrementa el grado del polinomio utilizado.
Relajación no lineal La solución numérica de sistemas en tres dimensiones usando colocación ortogonal para discretizar las ecuaciones, requiere de la generación de matrices muy grandes que se incrementan geométricamente en la medida que se incrementen los nodos de las mallas, por lo que es necesario encontrar algún método que no requiera del almacenamiento del Jacobiano, una de las alternativas es relajación no lineal o también conocida como Newton modi cado, cuyo algoritmo es [33]:
La velocidad de convergencia de la relajación no lineal depende del valor inicial de λ y, en problemas no lineales superiores, requiere muchas iteraciones para alcanzar la tolerancia pre jada. Sin embargo, las iteraciones se ejecutan rápidamente y son fáciles de codi car para plataformas en paralelo. Normalmente, se propone un valor inicial de λ = 0,5 para explorar la convergencia.
Código FORTRAN 90
El modelo representado por las ecuaciones (1) a (11) se resolvió por discretización espacial mediante colocación ortogonal con polinomios de Legendre Por otro lado, la discretización del tiempo se hizo con diferencias nitas para formar un esquema implícito de integración hacia adelante, para solventar la alta rigidez de las ecuaciones diferenciales. El sistema de ecuaciones algebraicas no lineales que se obtiene en cada etapa de integración se resuelve usando Relajación no Lineal. Con todo lo anterior se desarrollaron los códigos computacionales IMPLI-C2 e IMPLI-C3 usando lenguaje estándar FORTRAN 90.
Uso de Software comercial
Con el paso de los años y el auge de la era computacional se han desarrollado plataformas y paquetes de software para ayudar a resolver problema matemáticos complejos, estos paquetes ofrecen la ventaja de tener interfases de usuario simples y optimizaciones que mejoran la velocidad de los cálculos, sin embargo el uso de estos restringe al usuario a los métodos que están preprogramados en el software así como la eventual falta de conocimiento técnico de los métodos y ecuaciones que utiliza la plataforma.
Algunos de los programas más utilizados para resolver problemas de dinámica computacional de uidos (CFD) son ANSYS , COMSOL y MATLAB . ANSYS es un software de simulación ingenieril, desarrollado para funcionar bajo la teoría de elemento nito para estructuras y volúmenes nitos para uidos. COMSOL Multiphysics es un software de análisis CFD y resolución por elemento nito para varias aplicaciones físicas y de ingeniería, especialmente fenómenos acoplados o multifásicos. En esta investigación se utilizó COMSOL Multiphysics para validar los resultados que se obtienen con los códigos en FORTRAN 90.
Resultados
Se realizaron varias simulaciones para analizar el comportamiento de los per les de transferencia de momentum, calor y masa en el interior de silos agrícolas. En primera instancia, se simuló un silo pequeño de 1.83 metros de radio por 3.81 metros de altura lleno de sorgo, una semilla de producción común en la región, cuyos datos termodinámicos se encuentran en la Tabla 1.
Tabla 1. Datos termodinámicos del sorgo y del aire
Con las ecuaciones gobernantes en 2 dimensiones se realizó la simulación de un año completo usando FORTRAN 90, para simular las condiciones externas del silo en la frontera correspondiente a la pared y el techo se acopló el modelo ambiental, el suelo del silo se considera aislado y en el centro del silo se considera una condición de simetría, también se considera la generación volumétrica de calor debida a la respiración del grano. A continuación, se muestran los resultados:
 Figura 3. Perfiles de temperatura del silo en el día 1
Figura 3. Perfiles de temperatura del silo en el día 1La Figura 3 muestra las isotermas a distintas horas en el día 1 de la simulación. Se puede observar que el calor interno del silo aumenta conforme avanza el tiempo, empezando a aproximadamente 35 °C en el día y también se observa que a pesar de que la frontera se enfría debido al efecto de la temperatura ambiental, el calor se almacena dentro del silo por el efecto aislante del grano.
 Figura 4. Perfiles de temperatura del silo en el día 100
Figura 4. Perfiles de temperatura del silo en el día 100La Figura 4 muestra que el calor interno del silo aumenta conforme avanza el tiempo, empezando a aproximadamente 35 °C en el primer día y llegando a más de 40 °C después de 100 días, también se observa que a pesar de que la frontera se enfría debido al efecto de la ecuación de temperatura ambiental el calor se conserva dentro del silo por el efecto aislante del grano. Otra simulación que se realizó fue de un silo de mayor tamaño (5.3 m de radio por 13 m de altura) acoplando el modelo climático y las ecuaciones de radiación solar cuyos resultados se encuentran a continuación:
Figura 5. Per les de temperatura para el silo en el día 2 a diferentes horas
Se puede observar en la Figura 5 la formación de un núcleo caliente en la parte superior del silo que, dado a que es simétrico se formaría un anillo de calor en la parte superior del silo cilíndrico, además se puede observar que la simulación que solo contiene la temperatura ambiental la temperatura llega a aproximadamente 38 °C y la que tiene el modelo climático y el de radiación la temperatura aumenta hasta 42 °C lo cual demuestra que la radiación solar juega un papel importante en los procesos de transferencia internos en el almacenamiento de granos en silos.
Con propósitos de validación de los códigos FORTRAN 90, se resolvió el modelo matemático en 3D mediante el software COMSOL Multiphysics tomando como base el reporte de Jiménez-Islas et al., (2004) [9]. El sistema geométrico simulado consistió en un silo cilíndrico a escala industrial de 6 m de radio y una altura de 12 m, con una capacidad de 5000 toneladas. Las simulaciones de hicieron para un tiempo de almacenamiento de 42 días. Los resultados mostraron una excelente concordancia con lo reportado por Jiménez-Islas et al., (2004) [9]. Sin embargo, es importante mencionar que su estudio fue realizado en 2D empleando un silo a escala piloto de 1.83 m de radio y una altura de 3.81, con una capacidad aproximada de 60 toneladas (60940 kg de sorgo), por lo que en su reporte no se alcanzaron temperatura tal elevadas, como las reportadas en este trabajo.
 Figura 6. Distribución de temperatura (°C) durante el almacenamiento del sorgo.
Figura 6. Distribución de temperatura (°C) durante el almacenamiento del sorgo. Figura 7. Distribución de la humedad del aire durante el almacenamiento del sorgo.
Figura 7. Distribución de la humedad del aire durante el almacenamiento del sorgo. Figura 8. Movimientos de convección del aire dentro del silo durante el almacenamiento del sorgo.
Figura 8. Movimientos de convección del aire dentro del silo durante el almacenamiento del sorgo.La Figura 6 muestra que el grano se calienta homogéneamente a las pocas horas de almacenamiento (t=5.6 h), alcanzando valores de temperatura óptimos para el desarrollo de algunos tipos de hongos, este calentamiento continúa en el transcurso del almacenamiento hasta alcanzar temperaturas de 55.8 °C, debido al calor que generan los granos por su metabolismo, incrementando el contenido de humedad intersticial del grano el cual es homogéneo en el sorgo, así, como en el aire con nado en el cono.
Con respecto a la convección del aire dentro del silo se encuentra que las corrientes de convección no son su cientes para enfriar el grano, debido a que el aire intergranular más caliente tiende a subir por la masa central del granel y genera el calentamiento excesivo de los granos en la parte superior del silo, mientras que al aire intergranular frio tiende a bajar con arrastre de humedad, formando calentamientos en la parte inferior del silo, provocando incubación de plagas de insectos, crecimiento de mohos, producción de micotoxinas y pudrición de los granos. Por esta razón, resulta necesario iniciar periodos de aireación durante las primeras horas de almacenamiento para comenzar a reducir la temperatura en todo el granel, para conservar la humedad del grano dentro de los parámetros adecuados de conservación y comercialización, y con esto evitar el riesgo del calentamiento, daños al grano y presencia de plagas. Cabe mencionar que esta práctica se realiza generalmente tomando como base la experiencia o la intuición del productor.
En la Figura 7 se observa la distribución de la humedad intersticial del aire al inicio de la dinámica se observa que aire que se encuentra en el cono tiene la humedad inicial del aire (0.012 kg de agua/kg a.s.), mientras que la humedad del aire intersticial aumentando rápidamente a 0.015 kg de agua/kg a. s. debido al calor generado por la respiración del sorgo, durante el resto de la dinámica se alcanza el equilibrio entre el agua contenida en el grano y la contenida en aire intergranular. A la vez se va estableciendo el equilibrio entre el aire intergranular con el aire del cono, alcanzando valores máximos de 0.0314 kg de agua/kg a.s. Lo que representa un aumento de humedad del aire del 38% que representa la cantidad de humedad perdida por el sorgo debido al calentamiento excesivo.
Por último, en la Figura 8 se observa la dinámica de los per les de velocidad del aire intersticial durante el tiempo de almacenamiento. Se puede observar que al inicio de la dinámica las velocidades mínimas y máximas se encuentran en las paredes opuestas del silo este fenómeno se debe principalmente al gradiente de temperaturas impuesto sobre las paredes del silo. Posteriormente al continuar con la dinámica la convección natural del aire comienza a desarrollarse en el centro del silo manteniendo los granos tibios en la parte inferior del granel; el aire intergranular más caliente tiende a subir por la masa central del granel y genera un calentamiento del grano de los granos en la parte superior del granel. Entonces al condensarse la humedad en la parte superior del silo, provoca literalmente una lluvia que proviene del techo del silo. Esto ocasionará con el tiempo que pudiese manifestarse germinación de granos, calentamiento, acumulación de plagas de insectos, crecimiento de mohos, producción de toxinas y pudrición del grano. En la práctica, se aplica movimiento del grano o aireación con aire ambiental o aire frío para eliminar el calor acumulado en los granos, lo que permite inferir que la predicción de la dinámica de almacenamiento favorecerá un uso racional de la aireación con el consiguiente ahorro de energía.
Los resultados obtenidos a través de simulaciones en dos y tres dimensiones, utilizando tanto FORTRAN como COMSOL, brindan una perspectiva convincente de los procesos internos en el almacenamiento de granos en silos. Estos hallazgos no solamente proporcionan información crucial sobre la distribución de temperatura y la acumulación de calor a lo largo del tiempo, sino que también proporcionan evidencia sobre la eventualidad de temperaturas elevadas en el interior de los silos y sus efectos perjudiciales para los granos almacenados.
En la simulación de un año completo en un silo de dimensiones específicas, se observó un aumento progresivo de la temperatura interna, superando los 40 °C. Este aumento térmico representa un riesgo significativo, ya que temperaturas elevadas en un silo pueden desencadenar procesos de degradación y pérdida de calidad del grano. La acumulación de calor, especialmente en la parte superior del silo, puede propiciar la proliferación de hongos y micotoxinas, comprometiendo la seguridad alimentaria y la viabilidad comercial de los granos almacenados.
La simulación de un silo de mayor tamaño demostró la formación de un núcleo caliente en la parte superior, un fenómeno que, junto con temperaturas externas elevadas, puede generar condiciones propicias para la proliferación de hongos o de insectos. La inclusión de modelos climáticos y de radiación solar resalta la necesidad de considerar factores externos, ya que las temperaturas altas no solo afectan la calidad del grano, sino que también pueden desencadenar fenómenos adversos como la germinación, el deterioro del grano o la pérdida de materia seca.
Finalmente, con los resultados de esta modelación es posible abordar estudio de los fenómenos de transporte asociados al secado y almacenamiento de granos en silos, así como la dinámica de la aplicación de fumigantes. Todo esto conlleva al diseño termodinámico de silos que incluye factores como: 1) Predicción de patrones de ujo, per les de temperatura y concentración de humedad, 2) Cálculo de tiempo de secado y flujos de aire, 3) Dosis óptimas de agentes fumigantes, 4) Predicción de situaciones adversas en el almacenamiento de granos como son los puntos calientes y regiones donde exista estancamiento del aire o condensación de humedad, con el n de prevenir germinación del grano y/o infestación por hongos o insectos.
Editora en jefe: Dra. Martha Aguilar Trejo. Gestor editorial: Dr. Enrique Aguilar Vargas. Las opiniones expresadas en cada documento de esta publicación no reflejan necesariamente la opinión del equipo editorial ni de la institución. Se autoriza al reproducción total o parcial de los textos publicados, siempre y cuando se cite la fuente completa y la dirección electrónica de la publicación. ©️ COEPES GUANAJUATO, 2024