Control del Proceso, El camino para la mejora continua
Publicado: 18 de octubre de 2013
Fuente: José Carlos López Galitzia, Ing. Mecánico. Gerente de Planta de Aves Reproductoras de Centroamérica, S.A. División Alimentos Balanceados, del Grupo PAF en Guatemala C.A.
Se dice que los alimentos balanceados son una combinación de ingredientes mezclados uniformemente para aportar a los animales una dieta que contenga todos los nutrientes esenciales y necesarios para su sano desarrollo y/o la óptima producción de carne, leche, huevo o crías.
Actualmente también se exige que sean elaborados con las más estrictas normas de calidad y de inocuidad para garantizar que cumplan con los objetivos para los cuales son diseñados.
Entonces, desde su diseño, fabricación y distribución, los fabricantes deben asegurar que las dietas cumplan con esta función.
Para lograr todo esto, se requiere de una vigilancia estricta de todos y cada uno de los procesos por los que pasan los ingredientes hasta convertirse en alimentos terminados y son entregados a sus consumidores finales.
Esta vigilancia es más sencilla aplicando herramientas estadísticas que nos indiquen en donde estamos colocados dentro del objetivo final.
Entonces los procesos pueden ser controlados y analizados observando tendencias, capacidades y factores que nos ocasionan descontrol.
Existen varias herramientas estadísticas que aplican a procesos dependiendo de la información que necesitemos adquirir:
- Diagramas de Flujo
- Gráfica de Pareto
- Diagramas de Causa y Efecto
- Gráficas de Tendencia
- Histograma de Frecuencia
- Gráficas de Control
- Capacidad de Proceso
Y otras técnicas que nos pueden ayudar a encontrar los puntos en donde debemos enfocarnos para establecer mejoras en los procesos.
DIAGRAMAS DE FLUJO
Un Diagrama de Flujo es una representación gráfica que muestra todos los pasos de un proceso. Este tipo de diagramas proveen importante información de cómo los diferentes pasos de un proceso se relacionan entre sí. Además de lo anterior, también pueden ayudarnos a localizar aquellos pasos en donde puedan darse factores de descontrol de nuestros procesos.
GRÁFICAS DE PARETO
Una Gráfica de Pareto es una forma especial de gráfica de barras verticales las cuales nos ayudan a determinar cuáles problemas resolver y en qué orden. Normalmente la gráfica representa los problemas más importantes con barras más grandes, mismas que son en las que debemos poner enfoque ya que es muy frecuente que solucionando el 20% de los problemas, desaparecen el 80% de los efectos.
Ejemplo:

En este ejemplo, si reducimos los paros por problemas de mantenimiento, habremos reducido las causas en un 25%.
Esta herramienta estadística puede ser utilizada para situaciones como Paros de Producción por causa, Costos de fabricación, fallas de maquinaria, etc.
DIAGRAMAS DE CAUSA Y EFECTO
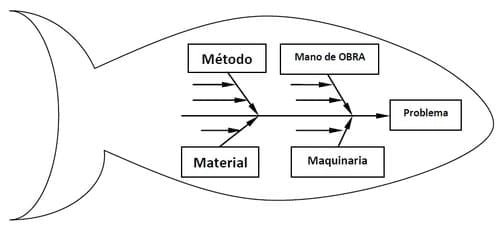
Los Diagramas de Causa y Efecto fueron desarrollados para representar la relación que existe entre algunos “efectos” y sus posibles “causas”
Estos diagramas también son conocidos como “de espina de pescado”. Cuando tenemos algunos problemas para resolver la mejor manera es hacerlo ordenadamente por lo que pondremos a cada lado los puntos en donde pudieran originarse tales problemas, entonces utilizamos el método de las “4 M”, Mano de obra, Métodos, Materiales y Maquinaria. Ahora, por medio de una “Tormenta de Ideas” (que es otra herramienta estadística) analizamos y anotamos las causas probables de los problemas, sin obviar ninguno.
GRÁFICAS DE TENDENCIA
Este tipo de gráficas se utilizan para visualizar el comportamiento de los datos a través de un periodo de tiempo.
Este tipo de gráficas son las más fáciles de construir ya que únicamente hace falta colocar los valores medidos en la gráfica y colocar una línea de promedio y una línea de tendencia.
Si este tipo de gráficas se analizan a intervalos lo suficientemente cortos pueden asegurar estabilidad de los procesos al facilitar la decisión de tomar acciones preventivas que eviten que el proceso se salga de control.

Parámetros como el rendimiento de las máquinas, el ausentismo, la rotación del personal, la generación de reprocesos o mermas, etc., pueden ser analizadas con este tipo de gráficas.
HISTOGRAMAS DE FRECUENCIA
Un Histograma de Frecuencia toma los datos medidos y muestra su comportamiento en una distribución normal.

Una distribución normal muestra que la mayoría de los datos están en la barra central y algunos datos quedan a los lados de esta barra. Desde luego, mientras más datos queden al centro de la curva implicará que el proceso es más estable y que es capaz de cumplir con las especificaciones del cliente.
Este tipo de gráficas se construyen a partir de colocar cada dato medido dentro de un rango de valores y después contar cuántos datos quedan en cada rango, de esa manera puede graficarse. Por ejemplo:

Con esta herramienta podemos analizar parámetros como tamaño de partículas, largo de pellets, peso de sacos, etc.
GRÁFICAS DE CONTROL
Una Gráfica de Control es una gráfica de tendencia que posee además límites de control (superior e inferior) arriba y debajo de una línea de promedio. Estos límites se calculan procesando los datos medidos

PASOS EN LA CONTRUCCIÓN DE UNA GRÁFICA DE CONTROL Y FORMULAS CRÍTICAS
Gráfica de Control Variable:
Cuando las muestras se expresan en unidades cuantitativas de medida, por ejemplo, Longitud, peso, tiempo etc.
Graficando el promedio & Rango de los datos obtenidos
Cálculo del promedio (X) y Rango de cada Subgrupo:

Cálculo del Rango promedio (R) y el promedio del proceso (X): -

Cálculo de los límites de control:


PASOS PARA LA CONTRUCCIÓN DE GRÁFICAS DE CONTROL Y FORMULAS CRÍTICAS
Gráficas de Control por Atributos:
Cuando la muestra refleja características cualitativas, por ejemplo; defectuoso/no, pasa/no pasa.
La gráfica ρ: = Proporción Defectuosa


La Gráfica c = Numero de noconformidades con tamaño constante de muestra.

La Gráfica u = Numero de noconformidades con tamaño variable de muestra


Esta fórmula crea límites de control cambiantes. Para evitar esto, utilice Tamaños de Muestra Promedios 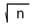 para estas muestras que son ±20% del tamaño promedio de muestra. Calcule límites individuales para muestras que excedan ± 20%.
para estas muestras que son ±20% del tamaño promedio de muestra. Calcule límites individuales para muestras que excedan ± 20%.
INTERPRETACIÓN DE LAS GRÁFICAS DE CONTROL
Se dice que los procesos están “fuera de control” si:
1. Uno o más puntos caen fuera de los límites de control
2. Cuando , disidiendo la gráfica de control en zonas como las mostradas abajo:

Se debe notar y examiner que cambió y probablemente hacer ajustes en el proceso si:
a) Dos puntos, de tres puntos consecutivos, están en el mismo lado de la línea central en la Zona A o cerca.
b) Cuatro puntos, de cinco puntos sucesivos, en el mismo lado de la línea central en la Zona B o cercana.
c) Nueve puntos sucesivos en un solo lado de la línea central.
d) Seis puntos consecutivos en dirección ascendente o descendente.
e) Catorce puntos de manera alternada hacia arriba y hacia abajo.
f) Quince puntos en la Zona C (Arriba y abajo de la línea central)
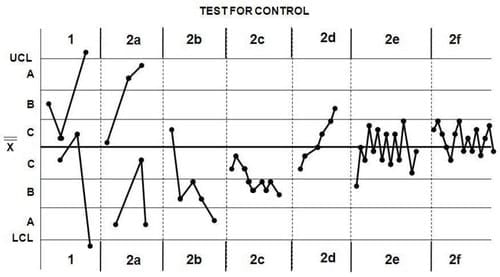
Como puede verse, este tipo de Gráficas puede utilizarse para verificar casi cualquier proceso y determinar si está en control o no.
CAPACIDAD DEL PROCESO
Tener un proceso dentro de control no es suficiente ya que un proceso “en control” puede producir malos productos. Las verdaderas mejoras de los procesos se logran balanceando repetitividad y consistencia con la capacidad de lograr las especificaciones de los clientes, eso es conocido como la Capacidad del Proceso.
FÓRMULAS PARA CALCULAR LOS ÍNIDCES DE CAPACIDAD DEL PROCESO
Cp es un índice de capacidad de proceso simple que relaciona la dispersión permisible de los límites de especificación (es decir, la diferencia entre el límite superior de especificación, USL y el límite inferior de especificación, LSL) a la medida de la variación real o natural, del proceso, representado por 6σ, donde σ es la desviación estándar del proceso.
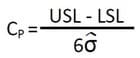
σ puede estimarse a partir de una gráfica de Control:
σ = R / d2
donde R = el promedio de los rangos de los subgrupos
d2 = un valor presentado basado en el tamaño de la muestra del subgrupo
Factores para σ estimado:

 | Las variaciones del proceso exceden los límites de especificación lo que implica que existen defectuosos. |
| El proceso está justo encontrando las especificaciones. Un mínimo de 0.3% defectuosos puede aparecer, o más si el proceso no está centrado. | |
| Las variaciones del proceso son menores que los límites de especificación; sin embargo pueden aparecer defectuosos si el proceso no está centrado al valor esperado. |
Mientras que CP relaciona la dispersión del proceso en relación con el rango de las especificaciones, NO da una visión de qué tan bien el proceso logra un promedio, X, centrado al valor esperado. CP se refiere a menudo como una medida del proceso “potencial”.
Los índices de capacidad de proceso CPt y CPu (por un lado) y CPk (para dos límites de especificación a ambos lados) mide no solo la variación del proceso con respecto a las especificación permitida, también toman en cuenta la localización del promedio del proceso. CPk se considera como una medida de la “capacidad” del proceso y es tomada como la más pequeña entre CPt o CPu.
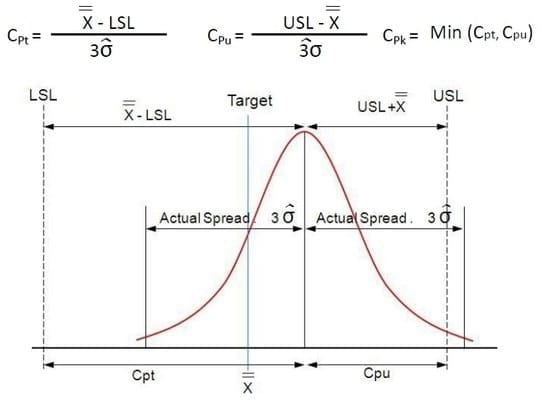
Si el proceso es casi normal y en control estadístico, CPk puede utilizarse para estimar el porcentaje previsto de material defectuoso.
Esta herramienta estadística es muy útil cuando queremos saber si nuestros procesos son capaces de lograr las especificaciones de nuestros clientes de manera consistente, por ejemplo: durabilidad de pellet, pellet por gramo, hidroestabilidad, % de finos, peso de sacos, y un amplio etcétera.
Existen otras herramientas estadísticas que pueden utilizarse igualmente para ayudarnos a controlar y mejorar nuestros procesos, pero recuerde que el seguimiento a los índices medidos en periodos cortos de tiempo pueden ayudarnos mucho a ejercer medidas preventivas, antes que correctivas para asegurar la calidad e inocuidad de nuestros productos en beneficio de nuestros clientes.
Temas relacionados:
Mencionados en esta noticia:
Vitali Alimentos - Grupo PAF
Recomendar
Comentar
Compartir
11 de junio de 2014
Excelente información como una recopilación de las herramientas básicas para lograr las mejora continua. Tambien estoy de acuerdo con algunos comentarios en que estas herramientas son fundamentales para el personal lider de primer nivel. Pero lo mas importante para lograr estas mejoras es la gente de operación (personal no experto en las herramientas de mejora), pero son quienes estan permanentemente manejando los equipos en proceso. Considero que con las herramientas actuales de comunicación (computadoras, tablets, teléfonos, etc), estas herramientas de mejora continua podrían llegar al personal de operación ya aterrizadas y en tiempo real, a partir de la información que ellos mismos estan generando y capturando. Lo cual permitiría corregir de inmediato cualquier desviación en forma preventiva.
Felicidades Ing. Carlos López Galitzia.
Recomendar
Responder
Vitali Alimentos - Grupo PAF
31 de octubre de 2013
Muy interesantes las opiniones de Ricardo y las comparto. Para poder alinear a la organización en el control de proceso es necesario diseñar el método de recuperación de datos en cada etapa importante del proceso que queremos controlar. La capacitación al personal involucrado es esencial para el éxito del proyecto. El diseño de formatos para el registro de los datos también juega un importante papel y la frecuencia con que los datos deban ser registrados.
Lo que hace que este tipo de herramientas otorguen su valor es la frecuencia como los responsables del proceso analicen los datos y los procesen de manera que descubran los puntos débiles y los corrijan oportunamente. La labor no es fácil, es laboriosa, pero sus resultados son espectaculares.
Recomendar
Responder
31 de octubre de 2013
Innovación en infraestructura = innovación en organización. No es un asunto de teoría de control sino de teoría organizacional. Planificar, organizar, sistematizar y la gerencia del todo hay que hacerla con plena conciencia. La conciencia está íntimamente ligada a la realidad. Ello implica conocer y entender que lo que se maneja no es una cosa sino un ente vivo que debe tener causas y que por delante de las causas están las personas que integran la organización. Organización no es estructura. Ésta es solo uno de sus elementos. Las estructuras unen los sistemas y en sus nodos se colocan personas para administrar un proceso (consumen recurso y producen resultados). Los sistema de control como los descrito por el autor de este tema, el Ing. López,son elementos que tienden a describir lo que sucede en la realidad. El asunto crítico es como se alinea la organización (todos sus elementos) con la nueva realidad que se quiere crear. Más allá también y como primer paso, determinar cual el estado deseado de desempeño organizacional, es fundamental. Este primer paso de planificación, es la piedra angular del proceso de aprendizaje.
Recomendar
Responder
29 de octubre de 2013
Me parece interesante la teoría de control, y para realizar los cambio en la media que acciones debemos tomar
Recomendar
Responder
24 de octubre de 2013
Muy buena la recopilación de herramientas asociadas a los enfoques de calidad total. Incurro en este comentario ya que tendemos a olvidar que las organizaciones son entes vivos. Consecuentemente, en una capa (nivel) muy superior están las Ideas Rectoras, la Teoría, Métodos y Herramientas y finalmente, la Innovación en Infraestructura. Estas herramientas y su implantación forman parte del ultimo elemento, Innovación en Infraestructura y son sólo una pequeña parte de ella. En consecuencia, de no asegurar que los otros elementos ya están alineados, el proceso de implantación de Calidad Total, no funcionará, tal como sucede en la mayoría de las empresas en el ambiente latino.
Recomendar
Responder


REAM
REAM y el Congreso Internacional de Rendering han decidido unir fuerzas para realizar la mayor convención para la industria agroalimentaria y del rendering
Enlace recomendado

¿Quieres comentar sobre otro tema? Crea una nueva publicación para dialogar con expertos de la comunidad.



.jpg&w=3840&q=75)








