Balance térmico en ganado de engorda europeo y cebú
Publicado: 3 de abril de 2018
Fuente: R. D. Sainz, V. A. Thompson, L.G. Barioni, T. R. Rumsey, J .G. Fadel. Universidad de California, CA, USA.
INTRODUCCIÓN
El estrés térmico en el ganado de engorda produce grandes pérdidas en la producción. Las respuestas fisiológicas al estrés por calor incluyen la vasodilatación cutánea, sudoración, aumento de la respiración y disminución del consumo. Una reacción inicial al aumento de la la temperatura es la vasodilatación, lo que aumenta el flujo de sangre a la superficie de la piel para llevar calor a la superficie de la piel y así aumentar la pérdida de calor por convección (Finch 1985). Aumentos en la sudoración y en la tasa de respiración también aumentan la pérdida de calor latente por el animal (Allen, 1962, Thomas & Pearson, 1986; Gaughan et al., 1999). En última instancia, si estos procesos no logran compensar el exceso de calor en el cuerpo, se hace necesario una reducción en la producción de calor mediante la disminución de la ingestión de alimentos (Brown-Brandl et al., 2003; Beatty et al., 2006). En ese caso tenemos un animal que ingiere menos de su potencial productivo, y que al mismo tiempo tiene sus costes energéticos incrementados por la necesidad de eliminar calor del cuerpo. La incrementación de las pérdidas de calor, a través de aumentos en la vasodilatación y en las tasas de respiración y de sudoración, también aumenta el coste de mantenimiento del animal. La disminución de la ingestión de pienso limita aún más la cantidad de energía y nutrientes dirigidos hacia el crecimiento o a la producción de leche, lo que resulta en una pérdida económica para los productores. Debido a las pérdidas económicas por el estrés térmico, los índices de temperatura-humedad (THI; Figura 1) fueron creados para estimar el nivel de estrés por calor del animal. El THI, propuesto por Thom & Bosen (1959), toma en cuenta la temperatura y la humedad relativa para determinar el nivel de estrés por calor para el animal. Sin embargo, estos índices no tienen en cuenta los procesos físicos y fisiológicos, por tanto, tienen limitaciones para la predicción de las respuestas fisiológicas y de producción frente a diversas opciones de manejo 2 y de mitigación. Esos índices tampoco consideran el efecto del tiempo, sin embargo sabemos que el animal puede suportar una situación de exceso de calor por algunas horas, desde que tenga una oportunidad posterior de disipar ese calor. Por ejemplo, la utilización de sombras, abanicos, y/o duchas, pueden, en determinadas situaciones, mejorar el estado y la productividad d los animales, pero tenemos herramientas limitadas para analizar sus relaciones costo-beneficio.
En este trabajo, describimos un modelo dinámico y mecanicista que simula el flujo de calor entre el animal y su ambiente, con los objetivos de 1) comprender los mecanismos del estrés térmico; 2) mejorar la predicción de las pérdidas en productividad; y 3) ayudar en la evaluación de la eficacia de posibles intervenciones de mitigación. Las variables consideradas son los flujos principales de calor entre el animal y su ambiente, con lo cual se calculan los cambios de temperatura en el cuerpo; el genotipo, específicamente las diferencias entre animales Bos indicus y Bos taurus; y los factores climáticos: temperatura, humedad relativa y absoluta, radiación / sombra, y viento.

MATERIALES Y MÉTODOS
El modelo funciona con el supuesto de que los valores de temperatura mínima y máximam diaria del aire, de radiación solar máxima, de presión de vapor (en cualquier momento durante el día) y de viento son conocidos. El modelo de equilibrio térmico es un modelo de tres nodos con tres variables de estado: los contenidos de calor en 1) el núcleo del cuerpo, 2) la piel, y 3) el pelo. La Figura 2 muestra una visión general del modelo con todos los flujos. El modelo tiene tres ecuaciones, siendo las dos primeras ecuaciones diferenciales y la tercera una ecuación algebraica, y tres incógnitas: las temperaturas del núcleo del cuerpo, de la piel y del pelo (Tb, Ts y Tc, respectivamente, °K). El modelo de balance térmico supone que el almacenamiento de calor en el pelo es pequeño y puede ser ignorado. Así, el cambio en el contenido de calor de la superficie del animal se pone a cero. Todas de los flujos de calor en el lado derecho de las ecuaciones diferenciales son funciones de Tb, Ts y Tc o funciones conocidas del tiempo bajo condiciones ambientales conocidas. Las transferencias de calor de los extremidades (cabeza y piernas) se dan a través de la piel y la superficie de pelo. La transferencia de calor a través de la piel y el pelo son multiplicados por la superficie total, lo que incluye apéndices y la papada. La suposición es que las resistencias dentro del pelo, de la piel y en el núcleo del cuerpo son uniformes y por tanto un valor medio puede multiplicarse por la superficie total para representar los flujos totales de calor. Los balances energéticos modelo se obtuvieron a través del método de diferencias finitas para problemas de conducción transitoria unidimensional (Myers, 1971). El modelo supone que las temperaturas en el núcleo del cuerpo, la piel y el pelo son uniformes, similar a Crosbie et al. (1961) y Stolwijk & Hardy (1966). Las ecuaciones que representan el cambio en el contenido de calor del núcleo del cuerpo, la piel y el pelo (todas en W), con respecto al tiempo están presentadas en Thompson et al. (2014a,b).
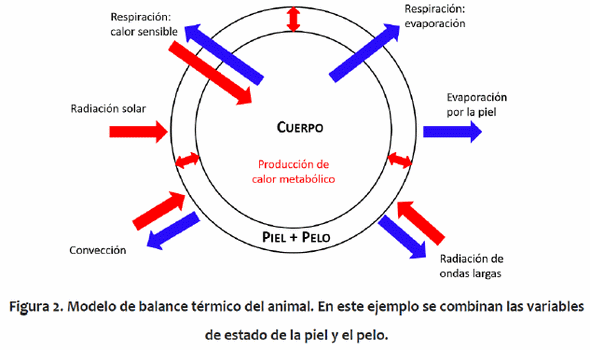
Los flujos de calor son modelados usando ecuaciones tomadas de la literatura. El contenido de calor del núcleo del cuerpo es una función de la producción de calor (HE, W) y los intercambios con la piel y el medio ambiente de dan mediante la conducción y la respiración, respectivamente. El flujo de calor desde el núcleo del cuerpo hasta la piel, se modeló con una ecuación estándar de flujo de calor (McArthur, 1987), que es una función de las temperaturas del núcleo del cuerpo y de la piel (Tb y Ts, °K) y la resistencia a la transferencia de calor. El efecto de la vasodilatación / la vasoconstricción tiene una relación lineal con la diferencia entre la temperatura referencia del núcleo del cuerpo y la temperatura del núcleo del cuerpo y está limitada por y valores máximos (Finch, 1985).
La pérdida de calor a través de la respiración se divide en convección y evaporación. El calor perdido a través de la convección respiratoria es una función de volumen de aire por respiración, la frecuencia de respiración, el calor específico del aire, la superficie del animal y las temperaturas del núcleo del cuerpo y del aire (McGovern y Bruce, 2000). También influyenla presión de saturación de vapor, la presión barométrica, y la temperatura del aire (McArthur, 1987).
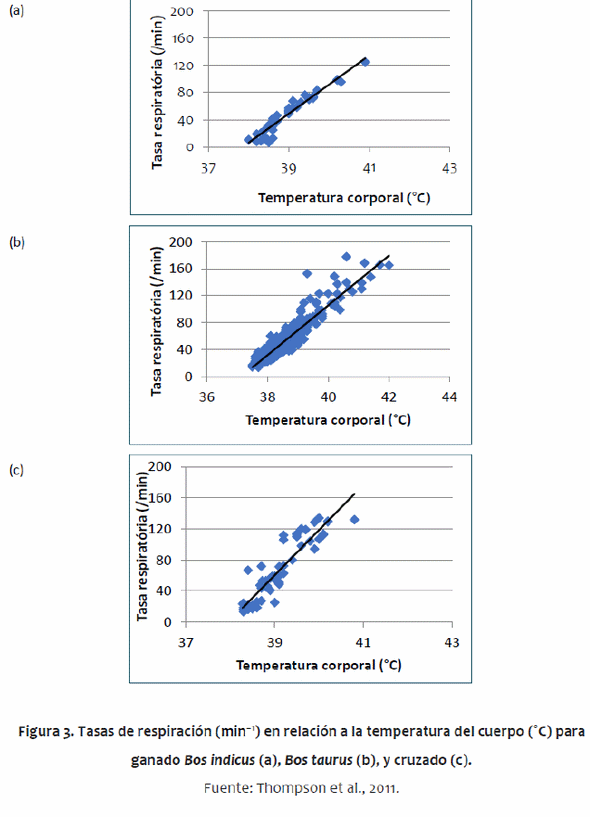
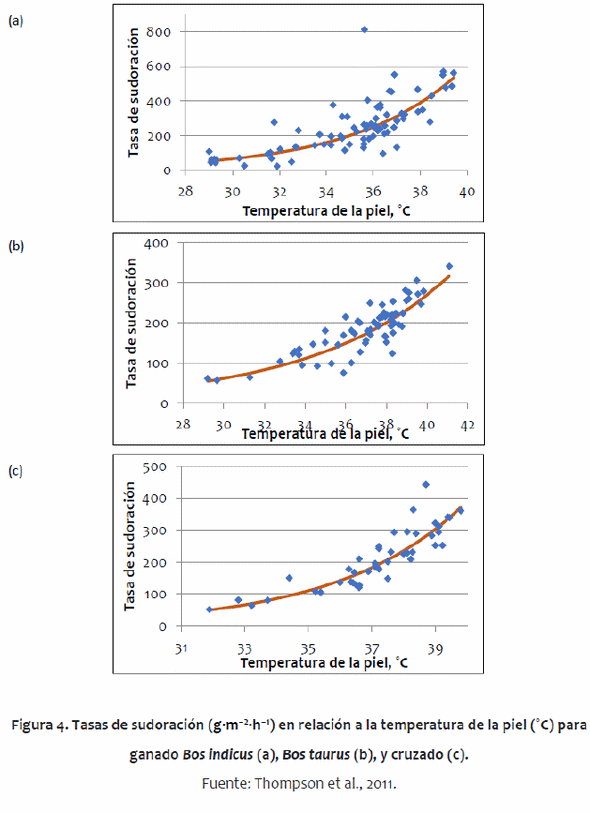
Algunos de los parámetros utilizados difieren entre genotipos de ganado, principalmente entre Bos indicus y Bos taurus. Bos indicus tienen algunas adaptaciones que los hacen más tolerantes a un clima tropical que los B. taurus, tal como una papada grande, una tasa de sudoración más alta, menos pelo, cambios en la distribución de reservas del cuerpo (gran joroba) y piel más gruesa (Pan, 1963; Hansen, 2004). El modelo da cuenta de la papada con mayor superficie. Un análisis preliminar mostró que la piel más gruesa de B. indicus no tuvo impacto en el balance térmico. Las diferencias metabólicas tienen poco impacto en el equilibrio térmico. McDowell et al. (1958) encontró que la joroba no tuvo ningún impacto en la regulación del calor, por lo tanto, esto no fue incluido en el modelo. Los parámetros del animal también permiten un amplio rango de madurez animal desde el destete hasta el ganado adulto. Los valores específicos para cada genotipo de los parámetros utilizados en el modelo se obtuvieron de un metaanálisis amplia de la literatura (Thompson et al., 2011). De acuerdo con esa metaanálisis, fueron desarrolladas ecuaciones específicas para ganado B. indicus y B. taurus, describiendo las tasas de sudoración (Figura 3) y de respiración (Figura 4).
La producción de calor metabólico (W) es modelado con el uso de ecuaciones adaptadas del NRC (1984), donde HeE es la producción de calor endógeno, HdE es el incremento calórico de la digestión, y HrE es el calor producido para la retención de energía en los tejidos. El incremento calórico de la digestión y la energía retenida se calculan a partir de las energías metabolizable (ME), neta para ganancia (NEg) y para mantenimiento (NEm) de la dieta (NRC 2000).
La pérdida de calor a través de la conducción al suelo no está incluida en este modelo, pues es más probable que el animal esté de pie durante el estrés térmico y en esta posición el contacto con el suelo es mínimo. La superficie del animal es calculada con una ecuación desarrollada para B. taurus (Brody, 1945) y es una función de la masa corporal. Johnston et al., (1958) encontraron que B. indicus tiene c. 12% más de superficie que B. taurus, por lo cual para B. indicus el parámetro es incrementado.
La radiación de onda larga es una función de las emisividades y temperaturas radiantes del animal y sus alrededores y la constante de Stefan-Boltzmann. Esto considera las emisividades en el infrarrojo para la superficie del animal (da Silva, 2000), y para el medio ambiente, y las emisividades del cielo. Las emisividades del cielo se calculan como una función de Ta (Brutsaert, 1975) y la cobertura de nubes (desde 0 hasta 1 donde 0 representa cielos claros y 1 representa la nubosidad completa; Crawford & Duchon, 1999). La temperatura radiante de los alrededores se calcula como la media del cielo y la tierra, de acuerdo con a la ecuación de Magnus Tetens (Murray, 1967).
La convección en la superficie del animal se calcula por la diferencia de temperatura entre el pelo y el aire dividido por la resistencia a la transferencia de calor por convección, lo cual depende del tamaño del animal y disminuye a medida que aumenta la velocidad del viento (Turnpenny et al., 2000a,b). La radiación solar proviene de tres fuentes: radiación directa, radiación difusa, y radiación reflejada desde la superficie el suelo, todas en W/m2. La radiación absorbida es una función de los coeficientes de reflexión para el animal y el suelo, respectivamente, y el factor de forma. El factor de forma es una función del ángulo corporal del animal en relación con el sol y sus dimensiones corporales (Monteith & Unsworth, 2008) y se calcula como el cociente del área de sombra del animal y su área de superficie. El área de sombra del animal es una función de la longitud corporal del animal y el ángulo de altitud del sol.
El modelo fue codificado en Matlab (2010) y utilizó un solución de ecuación diferencial ordinaria incorporada (ode23t). Es capaz de manejar sistemas de ecuaciones diferenciales algebraicas (DAE) (Shampine et al., 1999). Los datos climáticos de entrada (temperatura, presión de vapor, radiación solar y la velocidad del viento) se obtuvieron de estaciones meteorológicas para 21-24 junio 2006 en Davis, CA (CIMIS, 2009). Los datos meteorológicos por hora, si están disponibles, pueden implementarse en el modelo, reemplazando las ecuaciones climáticas por rutinas de interpolación.
RESULTADOS Y DISCUSIÓN
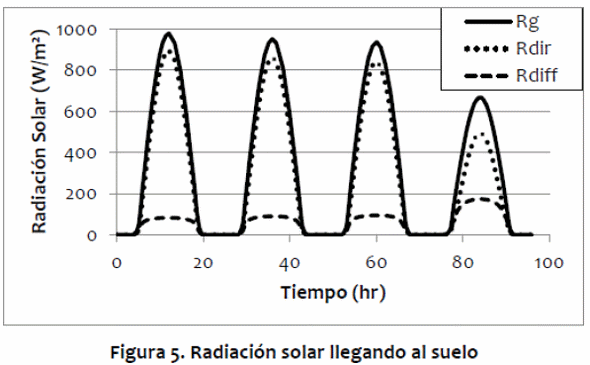
La Figura 5 muestra la radiación solar difusa, directa y total (W/m2) en el nivel del suelo. El pico de radiación difusa era mucho menos acentuado que el de la radiación directa y total. Por la mañana y por la tarde, el sol debe viajar a través de más de la atmósfera, y la proporción de radiación difusa a directa aumenta (Duffie y Beckman, 1991). En el cuarto día de simulación, la cantidad de radiación total y radiación directa cayó, pero la cantidad de radiación difusa aumentó, debido a la presencia de nubes en ese día. Las nubes pueden aumentar la proporción de radiación difusa de 0·1 a 1·0 de la radiación total (Sen, 2008).
El potencial de evaporación simulado se comportó como se esperaba, disminuyendo drásticamente con alta temperatura y alta humedad, como comúnmente visto en los trópicos húmedos (Figura 6). Cuando la humedad relativa es baja, la evaporación potencial aumenta a medida que la temperatura del aire sube, ya que la potencial de humedad absoluta aumenta con la temperatura del aire. Sin embargo, cuando hay humedad relativa alta, el potencial de evaporación disminuye a medida que aumenta la temperatura del aire. En ese caso, el gradiente de presión de vapor disminuye a medida que aumenta la temperatura del aire, y se hace más difícil para el animal perder calor a través de la evaporación de agua.
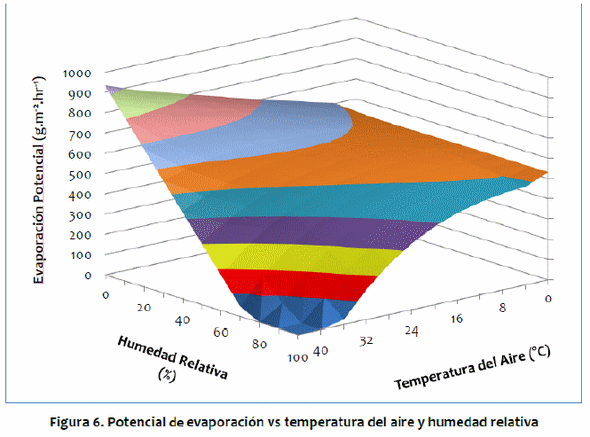
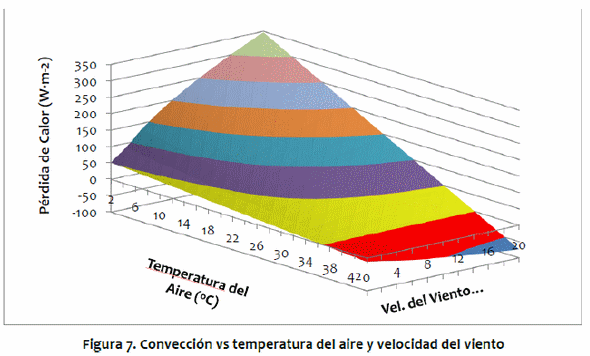
La Figura 7 muestra el gráfico de la pérdida convectiva de calor por la superficie del animal en relación a la temperatura del aire y la velocidad del viento. Cuando la temperatura del aire es baja, la velocidad del viento aumenta la pérdida de convección experimentada por el animal. Por el contrario, a altas temperaturas del aire, la velocidad aumenta la ganancia de calor por convección. Los resultados obtenidos por McArthur (1991) y Gebremedhin (1987) exhibieron relaciones similares entre la pérdida convectiva de calor, la temperatura del aire y la velocidad del viento. El viento disminuye la resistencia a la transferencia convectiva de calor; así, cuando la temperatura del aire es baja y el animal está perdiendo calor debido a la convección, cualquier aumento en la velocidad del viento aumentará la tasa de esta pérdida, pero cuando la temperatura del aire es alta y el animal está ganando calor debido a la convección, la velocidad del viento aumenta la tasa de esta ganancia.
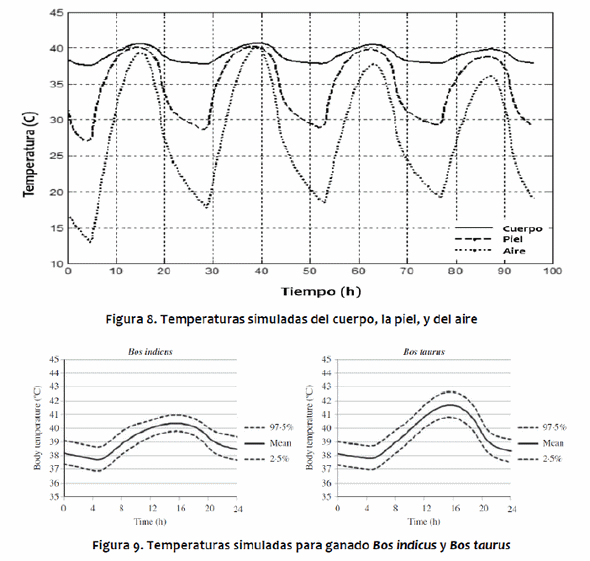
Las simulaciones del modelo para B. taurus y B. indicus muestran que las temperaturas del núcleo del cuerpo, piel y pelo de los B. indicus son todas inferiores a los B. taurus, debido a sus adaptaciones a las condiciones climáticas calientes. Para ambos genotipos, las fluctuaciones en las temperaturas diarias de la piel y del pelo están ligeramente desviados de los de la temperatura del aire, debido al impacto de la radiación solar (Figura 8). La temperatura máxima del aire ocurrió alrededor de las 15:00 h, mientras que la radiación solar máxima ocurrió al mediodía. El aumento de la carga solar animal resultó en un aumento en la temperatura del pelo ligeramente antes del aumento de la temperatura del aire, y cuando la temperatura del aire disminuyó, la carga solar ya no era tan intensa, por lo que la temperaturadel pelo podría disminuir junto con la temperatura del aire. Para B. taurus, el mayor flujo entrante fue la absorción de radiación solar, que exhibió un pico alrededor del mediodía. El ganado B. indicus tuvo una menor absorción de la radiación solar debido al pelo blanco con reflectividad más alta (Figura 9). Para ambos genotipos, la evaporación cutánea y las pérdidas respiratorias representan la mayor parte de la pérdida de calor durante el día, especialmente cerca de las 16:00 h cuando la temperatura del aire alcanza su máximo. Las pérdidas de calor por radiación de onda larga y las por convección son mayores durante la noche y las primeras horas de la mañana, como se muestra en los estudios de Kibler & Yeck (1959), Kelly et al. (1954) y Gebremedhin (1987), quienes encontraron que, a medida que disminuye la temperatura del aire, aumentan las pérdidas de calor tanto por convección como por radiación de onda larga, mientras que la pérdida por evaporación disminuye. Bos taurus y B. indicus muestran tendencias similares, aunque los flujos para B. taurus son generalmente más altos debido a mayor estrés térmico y, por lo tanto, mayor necesidad de disipar exceso de calor.
CONCLUSIONES
El modelo actual integra conceptos y datos relacionados con los flujos de calor entre los animales y su medio ambiente. La formas y los parámetros de estas ecuaciones se basan principalmente en principios físicos, anatómicos y fisiológicos. El desarrollo futuro del modelo actual podría incluir la adición de un componente dinámico de producción de calor, que incluye el comportamiento alimenticio, una representación detallada de cobertura de nubes y precipitaciones, un componente de aspersión de agua, que debe incluye el tamaño de las gotitas y un componente de producción durante la gestación y la lactancia. Este modelo debe ser evaluado más detalladamente frente a datos más completos y extensos para evaluar su capacidad de predecir la temperatura del núcleo del cuerpo en respuesta a diferentes condiciones ambientales tanto para ganado B. taurus como B. indicus.
LITERATURA CITADA
ALLEN, T. E. (1962). Responses of Zebu, Jersey, and Zebu X Jersey crossbred heifers to rising temperature, with particular reference to sweating. Australian Journal of Agricultural Research 13, 165–179.
BEATTY, D. T., BARNES, A., TAYLOR, E., PETHICK, D.,MCCARTHY, M. & MALONEY, S. K. (2006). Physiological responses of Bos taurus and Bos indicus cattle to prolonged, continuous heat and humidity. Journal of Animal Science 84, 972–985.
BRODY, S. (1945). Bioenergetics and Growth: with Special Reference to the Efficiency Complex in Domestic Animals. New York: Reinhold.
BROWN-BRANDL, T. M., NIENABER, J. A., EIGENBERG, R. A., HAHN, G.L. & FREETLY, H. (2003). Thermoregulatory responses of feeder cattle. Journal of Thermal Biology 28, 149–157.
BRUTSAERT, W. (1975). Derivable formula for long-wave radiation from clear skies. Water Resources Research 11, 742–744.
CIMIS (2009). California Irrigation Management Information System Department of Water Resources. Sacramento, CA, USA: Office of Water Use Efficiency. Available from: http://wwwcimis.water.ca.gov/cimis/welcome.jsp (verified 30 May 2013).
CRAWFORD, T.M. & DUCHON, C. E. (1999). An improved parameterization for estimating effective atmospheric emissivity for use in calculating daytime downwelling longwave radiation. Journal of Applied Meteorology 38, 474–480.
CROSBIE, R. J., HARDY, J.D. & FESSENDEN, E. (1961). Electrical analog simulation of temperature regulation in man. IRE Transactions on Bio-Medical Electronics 8, 245–252.
DA SILVA, R. G. (2000). Introdução à Bioclimatologia Animal. São Paulo, Brazil: Nobel.
DUFFIE, J.A. & BECKMAN, W. A. (1991). Solar Engineering of Thermal Processes. New York: Wiley.
FINCH, V. A. (1985). Comparison of non-evaporative heat transfer in different cattle breeds. Australian Journal of Agricultural Research 36, 497–508.
GAUGHAN, J. B., MADER, T. L., HOLT, S. M., JOSEY, M.J. & ROWAN, K. J. (1999). Heat tolerance of Boran and Tuli crossbred steers. Journal of Animal Science 77, 2398–2405.
GEBREMEDHIN, K. G. (1987). Effect of animal orientation with respect to wind direction on convective heat-loss. Agricultural and Forest Meteorology 40, 199–206.
HANSEN, P. J. (2004). Physiological and cellular adaptations of zebu cattle to thermal stress. Animal Reproduction Science 82–83, 349–360.
JOHNSTON, J. E., HAMBLIN, F.B. & SCHRADER, G. T. (1958). Factors concerned in the comparative heat tolerance of Jersey, Holstein and Red Sindhi-Holstein (F1) cattle. Journal of Animal Science 17, 473–479.
MATLAB (2010). Matlab Version 7.8.0. Natick, MA, USA: MathWorks Inc.
BEATTY, D. T., BARNES, A., TAYLOR, E., PETHICK, D.,MCCARTHY, M. & MALONEY, S. K. (2006). Physiological responses of Bos taurus and Bos indicus cattle to prolonged, continuous heat and humidity. Journal of Animal Science 84, 972–985.
BRODY, S. (1945). Bioenergetics and Growth: with Special Reference to the Efficiency Complex in Domestic Animals. New York: Reinhold.
BROWN-BRANDL, T. M., NIENABER, J. A., EIGENBERG, R. A., HAHN, G.L. & FREETLY, H. (2003). Thermoregulatory responses of feeder cattle. Journal of Thermal Biology 28, 149–157.
BRUTSAERT, W. (1975). Derivable formula for long-wave radiation from clear skies. Water Resources Research 11, 742–744.
CIMIS (2009). California Irrigation Management Information System Department of Water Resources. Sacramento, CA, USA: Office of Water Use Efficiency. Available from: http://wwwcimis.water.ca.gov/cimis/welcome.jsp (verified 30 May 2013).
CRAWFORD, T.M. & DUCHON, C. E. (1999). An improved parameterization for estimating effective atmospheric emissivity for use in calculating daytime downwelling longwave radiation. Journal of Applied Meteorology 38, 474–480.
CROSBIE, R. J., HARDY, J.D. & FESSENDEN, E. (1961). Electrical analog simulation of temperature regulation in man. IRE Transactions on Bio-Medical Electronics 8, 245–252.
DA SILVA, R. G. (2000). Introdução à Bioclimatologia Animal. São Paulo, Brazil: Nobel.
DUFFIE, J.A. & BECKMAN, W. A. (1991). Solar Engineering of Thermal Processes. New York: Wiley.
FINCH, V. A. (1985). Comparison of non-evaporative heat transfer in different cattle breeds. Australian Journal of Agricultural Research 36, 497–508.
GAUGHAN, J. B., MADER, T. L., HOLT, S. M., JOSEY, M.J. & ROWAN, K. J. (1999). Heat tolerance of Boran and Tuli crossbred steers. Journal of Animal Science 77, 2398–2405.
GEBREMEDHIN, K. G. (1987). Effect of animal orientation with respect to wind direction on convective heat-loss. Agricultural and Forest Meteorology 40, 199–206.
HANSEN, P. J. (2004). Physiological and cellular adaptations of zebu cattle to thermal stress. Animal Reproduction Science 82–83, 349–360.
JOHNSTON, J. E., HAMBLIN, F.B. & SCHRADER, G. T. (1958). Factors concerned in the comparative heat tolerance of Jersey, Holstein and Red Sindhi-Holstein (F1) cattle. Journal of Animal Science 17, 473–479.
MATLAB (2010). Matlab Version 7.8.0. Natick, MA, USA: MathWorks Inc.
MCARTHUR, A. J. (1987). Thermal interaction between animal and microclimate: a comprehensive model. Journal of Theoretical Biology 126, 203–238.
MCARTHUR, A. J. (1991). Thermal-radiation exchange, convection and the storage of latent-heat in animal coats. Agricultural and Forest Meteorology 53, 325–336.
MCDOWELL, R. E., MCDANIEL, B.T. & HOOVEN, N.W. (1958). Relation of the rhomboideus (hump) muscle in zebu and European type cattle. Journal of Animal Science 17, 1229 (abstract).
MCGOVERN, R.E. & BRUCE, J.M. (2000). A model of the thermal balance for cattle in hot conditions. Journal of Agricultural Engineering Research 77, 81–92.
MURRAY, F.W. (1967). On the computation of saturation vapor pressure. Journal of Applied Meteorology 6, 203–204.
NRC (1984). Nutrient Requirements of Beef Cattle, 6th edn, Washington, DC: National Academy Press.
NRC (2000). Nutrient Requirements of Beef Cattle, 7th edn, Washington, DC: National Academy Press.
PAN, Y. S. (1963). Quantitative and morphological variation of sweat glands, skin thickness, and skin shrinkage over various body regions of Sahiwal Zebu and Jersey cattle. Australian Journal of Agricultural Research 14, 424–437.
SEN, Z. (2008). Solar Energy Fundamentals and Modeling Techniques: Atmosphere, Environment, Climate Change, and Renewable Energy. London: Springer.
SHAMPINE, L. F., REICHELT, M.W. & KIERZENKA, J. A. (1999). Solving index-1 DAEs in MATLAB and Simulink. SIAM Review 41, 538–552.
STOLWIJK, J. A. J. & HARDY, J. D. (1966). Temperature regulation in man – a theoretical study. Pflügers Archiv (European Journal of Physiology) 291, 129–162.
THOM, E.C. & BOSEN, J. F. (1959). The discomfort index. Weatherwise 12, 57–60.
THOMAS, C.K. & PEARSON, R. A. (1986). Effects of ambienttemperature and head cooling on energy-expenditure, food-intake and heat tolerance of Brahman and Brahman x Thermal balance model for B. indicus and B. Taurus Friesian cattle working on treadmills. Animal Production 43, 83–90.
THOMPSON, V. A., FADEL, J.G. & SAINZ, R. D. (2011). Metaanalysis to predict sweating and respiration rates for Bos indicus, Bos taurus, and their crossbreds. Journal of Animal Science 89, 3973–3982.
THOMPSON, V.A., BARIONI, L.G., RUMSEY, T.R., FADEL, J.G., & SAINZ, R.D. (2014a). The development of a dynamic, mechanistic, thermal balance model for Bos indicus and Bos taurus. Journal of Agricultural Science 152, 464–482.
THOMPSON, V.A., SAINZ, R.D., STRATHE, A.B., RUMSEY, T.R., & FADEL, J.G. (2014b). The evaluation of a dynamic, mechanistic, thermal balance model for Bos indicus and Bos taurus. Journal of Agricultural Science 152, 483–496.
TURNPENNY, J. R., MCARTHUR, A. J., CLARK, J.A. & WATHES, C.M. (2000a). Thermal balance of livestock 1. A parsimonious model. Agricultural and Forest Meteorology 101, 15–27.
TURNPENNY, J. R.,WATHES, C. M., CLARK, J.A. & MCARTHUR, A. J. (2000b). Thermal balance of livestock 2. Applications of a parsimonious model. Agricultural and Forest Meteorology 101, 29–52.
MCARTHUR, A. J. (1991). Thermal-radiation exchange, convection and the storage of latent-heat in animal coats. Agricultural and Forest Meteorology 53, 325–336.
MCDOWELL, R. E., MCDANIEL, B.T. & HOOVEN, N.W. (1958). Relation of the rhomboideus (hump) muscle in zebu and European type cattle. Journal of Animal Science 17, 1229 (abstract).
MCGOVERN, R.E. & BRUCE, J.M. (2000). A model of the thermal balance for cattle in hot conditions. Journal of Agricultural Engineering Research 77, 81–92.
MURRAY, F.W. (1967). On the computation of saturation vapor pressure. Journal of Applied Meteorology 6, 203–204.
NRC (1984). Nutrient Requirements of Beef Cattle, 6th edn, Washington, DC: National Academy Press.
NRC (2000). Nutrient Requirements of Beef Cattle, 7th edn, Washington, DC: National Academy Press.
PAN, Y. S. (1963). Quantitative and morphological variation of sweat glands, skin thickness, and skin shrinkage over various body regions of Sahiwal Zebu and Jersey cattle. Australian Journal of Agricultural Research 14, 424–437.
SEN, Z. (2008). Solar Energy Fundamentals and Modeling Techniques: Atmosphere, Environment, Climate Change, and Renewable Energy. London: Springer.
SHAMPINE, L. F., REICHELT, M.W. & KIERZENKA, J. A. (1999). Solving index-1 DAEs in MATLAB and Simulink. SIAM Review 41, 538–552.
STOLWIJK, J. A. J. & HARDY, J. D. (1966). Temperature regulation in man – a theoretical study. Pflügers Archiv (European Journal of Physiology) 291, 129–162.
THOM, E.C. & BOSEN, J. F. (1959). The discomfort index. Weatherwise 12, 57–60.
THOMAS, C.K. & PEARSON, R. A. (1986). Effects of ambienttemperature and head cooling on energy-expenditure, food-intake and heat tolerance of Brahman and Brahman x Thermal balance model for B. indicus and B. Taurus Friesian cattle working on treadmills. Animal Production 43, 83–90.
THOMPSON, V. A., FADEL, J.G. & SAINZ, R. D. (2011). Metaanalysis to predict sweating and respiration rates for Bos indicus, Bos taurus, and their crossbreds. Journal of Animal Science 89, 3973–3982.
THOMPSON, V.A., BARIONI, L.G., RUMSEY, T.R., FADEL, J.G., & SAINZ, R.D. (2014a). The development of a dynamic, mechanistic, thermal balance model for Bos indicus and Bos taurus. Journal of Agricultural Science 152, 464–482.
THOMPSON, V.A., SAINZ, R.D., STRATHE, A.B., RUMSEY, T.R., & FADEL, J.G. (2014b). The evaluation of a dynamic, mechanistic, thermal balance model for Bos indicus and Bos taurus. Journal of Agricultural Science 152, 483–496.
TURNPENNY, J. R., MCARTHUR, A. J., CLARK, J.A. & WATHES, C.M. (2000a). Thermal balance of livestock 1. A parsimonious model. Agricultural and Forest Meteorology 101, 15–27.
TURNPENNY, J. R.,WATHES, C. M., CLARK, J.A. & MCARTHUR, A. J. (2000b). Thermal balance of livestock 2. Applications of a parsimonious model. Agricultural and Forest Meteorology 101, 29–52.
Contenido del evento:
Temas relacionados:
Mencionados en esta noticia:
Recomendar
Comentar
Compartir
11 de abril de 2018
La verdad que es un tema muy apasionante y que debemos tener.en cuenta para optimizar nuestros resultados en los Hatos dedicados al engorde. Gracias por compartir su artículo.
Recomendar
Responder

¿Quieres comentar sobre otro tema? Crea una nueva publicación para dialogar con expertos de la comunidad.





